Das PhYsiK-sKriPt
Das PhYsiK-sKriPt ist ein im Aufbau befindliches digitales Buch ¸ber die Physik der hessischen Oberstufe.
Es soll mˆglichst gut verst‰ndlich in die physikalischen Zusammenh‰nge einf¸hren und so hessischen Sch¸lern unterrichtsbegleitend beim Verst‰ndnis helfen.
Das PhYsiK-sKriPt steht unter der folgenden Lizenz:
Es wurde von den folgenden Sch¸lern der Oberstufe verfasst (alphabetisch):
Charmaine Guse, Dominik K., Eva Noble, Laura Schneiderbauer, Lennart, Maximilian, Pascal, Patrick Kramer, Tobias, Vanessa, Victoria Liebel, Vincent, Yannik, Katharina, Christian D., Melissa, Dominik L.
Organisation und Struktur: Alexander Staidl
F¸r die Autoren gibt es die Autorenseite
Inhalt
- Existenz von 2 verschiedenen Ladungen, Abstoþende und anziehende Kr‰fte
- Gleichnamige Ladungen stoþen sich ab!
- Die Funktionsweise des Elektroskop
- Leiter und Nichtleiter
- Neutralisation von Ladungen
- Das Elektronengasmodell elektrischer Leiter
- Freie Beweglichkeit negativer Ladungen
- Influenz
- Die Influenzmaschine nach Kelvin
- Dipole
- Induzierte Dipole
- Faraday's Feldtheorie
- Feldlinienbilder von Punktladungen und Kondensatoren
- Elektrische Kr‰fte wirken tangential zu den Feldlinien
- Die Feldlinien enden senkrecht an der Oberfl‰che geladener metallischer Kˆrper
- Der Faraday'sche K‰fig
- Der Zusammmenhang zwischen Ladung, Kraft und St‰rke des E-Feldes
- Parallelen und Unterschiede zwischen elektrischem Feld und Gravitation
- Bewegungen senkrecht und diagonal zu den Feldlinien
- Definition der Spannung
- Untersuchung der Spannung zwischen Kondensatorplatten
- Potential und ƒquipotentialfl‰che
- Der Zusammenhand zwischen U, E und d beim Plattenkondensator
- Die Elektronenkanone
- Die Einheit Elektronenvolt
- Das Ablenksystem einer Brown'schen Rˆhre
- Der Zusammenhang zwischen Fl‰chenladung und Feldst‰rke
- Die Fl‰chenladung h‰ngt tats‰chlich nur vom Feld E ab!!
- Die Fl‰chenladungsdichte
- Der Zusammenhang zwischen Fl‰chenladungsdichte und Feldst‰rke
- Die Kapazit‰t eines Kondensators
- Die Dieelektrizit‰tszahl
- Mikroskopische Betrachtung von Isolatoren in elektrischen Feldern
- Parallelschaltung von Kondensatoren
- Reihenschaltung von Kondensatoren
- Reihenschaltung von Kondensatoren - Betrachtung der Ersatzkapazit‰t
- Die SI-Grundeinheiten
- Das elektrische Feld einer Punktladung
- Die Coulomb-Kraft
- [[#VergleichCoulombGravi | Vergleich der Coulombkraft mit der Gravitationskraft+}
- Transportarbeit zwischen 2 Punkten im Coulomb-Feld
- Spannung zwischen 2 Punkten im Coulomb-Feld
- Das Coulomb- Potential
- Die Kapazit‰t einer Kugel
- Potential zweier mit Polen verbundenen Dr‰hte
- Qualitative Bedeutung des elektrischen Stroms
- Die elektrische Stromst‰rke
- Begriff der elektrischen Leistung
- Berechnung der Leistung
- Die Einheit Kilowattstunden
- Der elektrische Widerstand
- Reihenschaltung von Widerst‰nden
- Parallelschaltung von Widerst‰nden
- Die in Kondensatoren gespeicherte Energie
- Die Energiedichte des elektrischen Feldes
- Potential an Widerstand und Kondensator
- Entladevorgang bei Kondensatoren
- Berechnung von Halbwertszeiten
- Ferromagnetische Stoffe
- Modell der Elementarmagnete
- Separation der Pole eines Magneten
- Kraft auf stromdurchflossene Leiter
- Die magnetische Flussdichte - ein Maþ f¸r die St‰rke magnetischer Felder
- Bestimmung der Masse von Elektronen
- Der Massenspektrograph
- Der Halleffekt
- Das Magnetfeld einer lang gestreckten Spule
- Induktion in einem geraden Leiterst¸ck
- Magnetischer Fluss und Flussdichte und deren anschauliche Bedeutung
- Induktionsspannung in Spulen
- Induktion auch ohne Bewegung?
- Elektrische Wirbelfelder
- Anwendungen elektrischer Wirbelfelder
- Der Zusammenhang zwischen Lenz'schem Gesetz & Energieerhalungssatz
- Die Induktivit‰t (oder auch Eigeninduktivit‰t)
- Selbstinduktion - Der Einschaltvorgang
- Ideenfindundung: Wie kann man Schwingungen mathematisch beschreiben?
- Definition der haromonischen Schwingung
1.: Existenz von 2 verschiedenen Ladungen, Abstoþende und anziehende Kr‰fte
Experiment: Jeder Sch¸ler zieht Gefrierbeutelstreifen auseinander, welche aneinander gehalten werden
Beobachtung und Vermutungen:
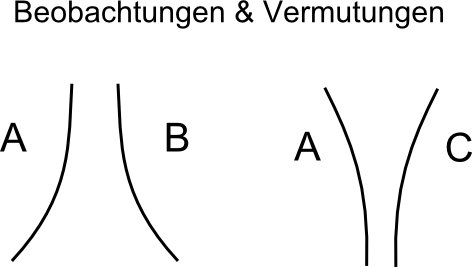
=> Es gibt zwei verschiedene Arten von Ladung, die entweder anziehnd oder abstoþende Kr‰fte aufeinander aus¸ben. Zur Unterscheidung bezeichnen wir sie mit "+" beziehungsweise mit "-".
Hypothesen: 1.1 Gleichnamige Ladungen stoþen sich ab, ungleichnamige ziehen sich an 1.2 Ungleichnamige Ladungen stoþen sich ab, gleichenamige ziehen sich an => Keine der Hypothesen kann durch dieses Experiment als falsch erkl‰rt werden. Dies verdeutlicht den Falsifizierungscharakter der Physik!
2.: Gleichnamige Ladungen stoþen sich ab!
Experiment: Es werden 2 Strohhalme werden zusammengedr¸ckt aufgeladen, sie haben also beide die gleiche Ladung
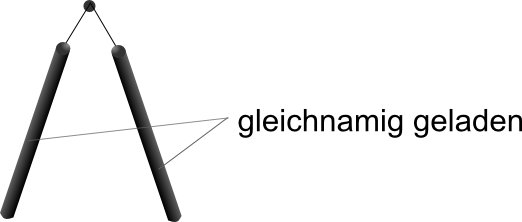
Schlussfolgerung: => Gleichnamig geladene Strohhalme stoþen sich ab, deshalb wird die Hypothese 1.2 verworfen!
3.: Die Funktionsweise des Elektroskop
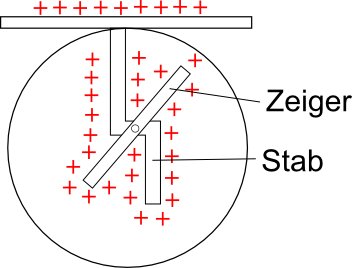
Ergebnis:
Wird ein Elektroskop geladen, so schl‰gt der Zeiger aus!
Erkl‰rung:
Wird das Elektroskop positiv geladen, bedeutet dies, dass ihm Elektronen entzogen wurden. Es gibt dadurch mehr positive Ladungen im gesamten Metall.
Das gleiche geschieht, wenn das Elektroskop negativ geladen wird. Diesmal befinden sich mehr Elektronen im Metall.
Der Elektroskopstab und der Zeiger sind gleich geladen und da sich gleichnamige Ladungen abstoþen schl‰gt der Zeiger aus.
Durch ein Elektroskop kann man also die elektrische Ladung nachweisen, jedoch nicht das Vorzeichen der aufgebrachten Ladung.
4.: Leiter und Nichtleiter
Kˆrper/Stoffe besitzen die Eigenschaft der elektrischen Leitf‰higkeit. Die Leitf‰higkeit basiert auf mehr oder weniger beweglichen/freien Elektronen in einem Stoff.
Man klassifiziert:
1. Leiter: Leiter kˆnnen die Ladungen weiterleiten. Dazu m¸ssen beweglich Ladungstr‰ger in einem Kˆrper vorhanden sein, die Ladung transportieren kˆnnen. Zu dieser Stoffgruppe z‰hlen die Metalle, wie zum Beispiel Eisen, Kupfer, oder Zink (etc.). Aber auch einige nicht metallische Stoffe kˆnnen Ladungen leiten. Dazu gehˆren unter anderem Graphit oder Aktivkohle.
2. Schlechte Leiter: Stoffe kˆnnen die Ladungen nur bedingt leiten, also lediglich schwach, wie zum Beispiel Wasser und andere Lˆsungen. Andererseits fallen in diese Kategorie auch Stoffe,dieelektrischen Strom z.B. in Abh‰ngigkeit der Temperaturleiten; sprich Leiter und Isolatoren sein kˆnnen.
3. Nichtleiter/Isolatoren: Isolatoren kˆnnen die Ladungen nicht weiterleiten, aufgrund ihrer atomaren/molekularen Struktur. Die Valenzelektronen liegen bei diesen Stoffen nicht "frei" vor, sondern befinden sich lediglich auf der Valenzelektronenschale des Atoms. Durch den positiven Kern werde sie auf dieser Bahn gehalten und kˆnnen im Gegensatz zu den Leitern keine Ladungen transportieren. Typische Isolatoren sind Plastik, Styropor, Glas, usw. Man findet diese z.B. an Stromkabeln, so kann man auch bei anliegender Spannung das Kabel anfassen ohne mit dem Strom in Ber¸hrung zu kommen.
5.: Neutralisation von Ladungen
Ein Gefrierbeutelstreifen wird getrennt und die beiden Streifenh‰lften werden auf die Platten unterschiedlicher Elektroskope gelegt. => Diese schlagen aus...
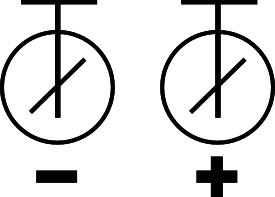
Nachdem die Platten miteinander kurz in Ber¸hrung gebracht werden, geht der Ausschlag zurr¸ck.
Die Ladungen ¸berlagern sich und neutralisieren ihre Wirkungen In diesem Fall m¸sste man sie auch wieder trennen kˆnnen. ==> Z.B. durch Reibung mit einem anderen Stoff (Reibungselektrizit‰t)
6.: Das Elektronengasmodell elektrischer Leiter
Annahmen :
- In metallischen Leitern existieren positive und negative LadungenDie positiven Ladungen liegen fest, die negativen Ladungen sind frei beweglich. Die negativen Ladungstr‰ger nennt man Elektronen.Metallische Kˆrper sind bei einem Elektronen¸berschuss negativ geladen, wohingegen bei einem Elektronenmangel die positiven Ladungen und der metallische Kˆrper ist positiv geladen.

7. Ziel: Kondensator, Aufladung durch Netzger‰t, Erkl‰rung von Strom auf Basis von Ladungen
8.: Freie Beweglichkeit negativer Ladungen
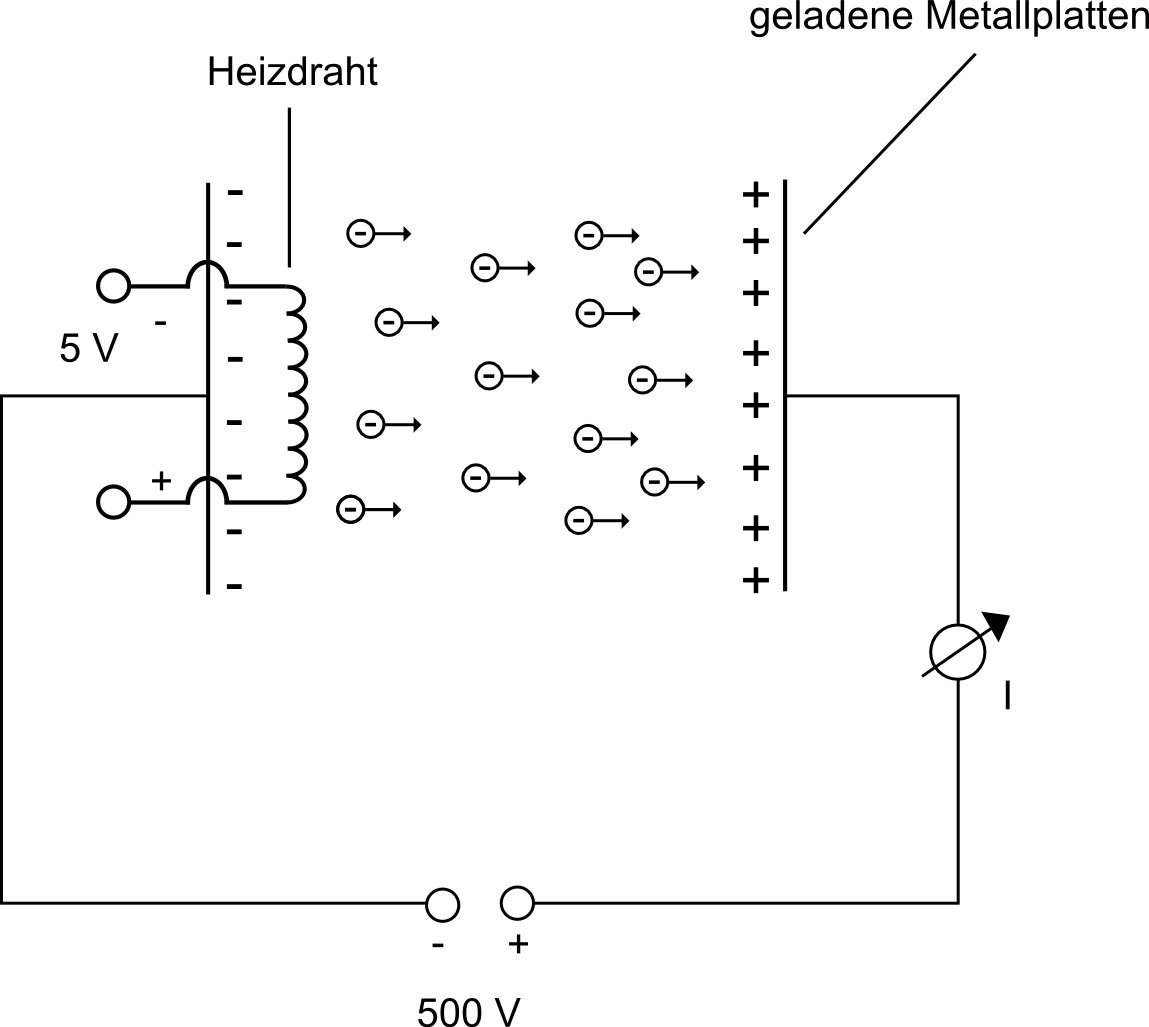
Das Strommessger‰t zeigt nur dann einen Ladungsfluss an, wenn die Platte auf der Seite des Strommessger‰tes positiv geladen ist. Das heisst, negative Ladungen treten aus dem Gl¸hdrat aus und werden zur "+"-Platte hin beschleunigt. L‰dt man die rechte Platte negativ auf, so zeigt das Messger‰t keinen Ladungsfluss an. Es treten demnach keine positiven Ladungstr‰ger aus.
9.: Influenz
Experiment: Eine geladene Folie wird einem neutral geladenem elektroskop angen‰hert, ohne es zu ber¸hren.
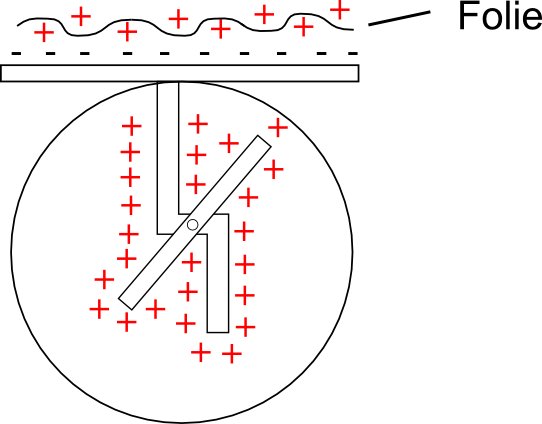
Das Elektroskop schl‰gt aus. Der Ausschlag geht zur¸ck, wenn die Folie wieder entfernt wird.
=> Die negativen Ladungen werden nach oben gezogen!
=> Beweis, dass neutrale Kˆrper sowohl aus negativen als auch aus positiven Ladungen bestehen, deren Wirkungen sich neutralisieren!
10.: Die Influenzmaschine nach Kelvin
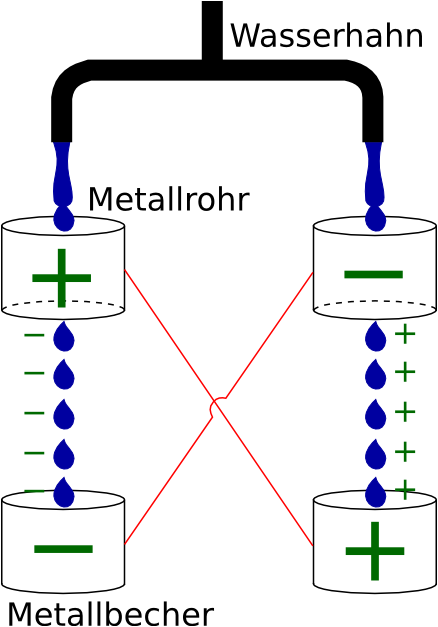
Durch Zufall befinden sich mehr Wassertrˆpfchen mit negativ Ladung
im rechten Wasserhahn. Diese Ladungen werden an das Rˆhrchen abgegeben.
--> Und zwar aus folgendem Grund: Wenn der Strahl in dem Rˆhrchen zu Tropfen zerreiþt, m¸ssen sich auch die zuf‰lligen Ladungen aufteilen. Dabei kann es ein, dass ein Elektronen ins Rˆhrchen ¸bergeht.
Dadurch l‰d sich diese negativ auf und da sie mit dem linken unteren Becher verbunden ist, werden die Ladungen auf diese beiden gleich verteilt.
Wenn nun rechts oben das Rˆhrchen negativ geladen ist, dann gibt es einen INFLUENZEFFEKT und es werden Elektronen noch aus dem Wasserstrahl zur¸ck in die Leitung getrieben. Dadurch fallen vermehrt positive Ladungen als Tropfen aus dem Hahn und diese landen dann auch in dem rechten unteren Becher.
Dieser l‰d sich also gleichfalls positiv auf. Genauso, wie das (durch das Kabel verbundene) obere linke Rˆhrchen. Auf der anderen Seite der Konstruktion, auf der linken Seite passiert also alles gleichzeitig wie rechts nur genau "umgekehrt".
Dies ist ein SELBSTVERSTƒRKENDER Effekt, der durch die Ladungstrennung unglaublich hohe Spannungen erzeugen kann.
So kann man, nach etwas Zeit zuerst zusehen, wie die Trˆpfchen so sehr abgelenkt werden, dass sie garnicht mehr unten ankommen und dann etwas sp‰ter sogar noch beobachten, dass sie wieder "nach oben" fliegen weil die Feldst‰rke eine grˆþere Kraft auf sie auswirkt als die Gravitation.
Tipp zum "Selberbauen": Die Maschine w¸rde auch ohne eine Startladung funktionieren, jedoch braucht man daf¸r etwas mehr Zeit. Wenn man sich nicht so sehr auf die Folter spannen will, gibt man einfach einem Becher eine geringe Startladung...
Das kann sogar eine durch ein Katzenfell erzeugte Ladung sein.
--> wenig gen¸gt bereits.
Auf einem ‰hnlichen Prinzip beruhend: z.B der Bandgenerator
Auch interessant: VIDEO ZUR KELVIN-MASCHINE

11.: Dipole
Exp.: Ein Wasserstrahl wird sowohl von einer positiv geladenen, wie von einer negativ geladenen Folie abgelenkt- und zwar zur Folie hin.
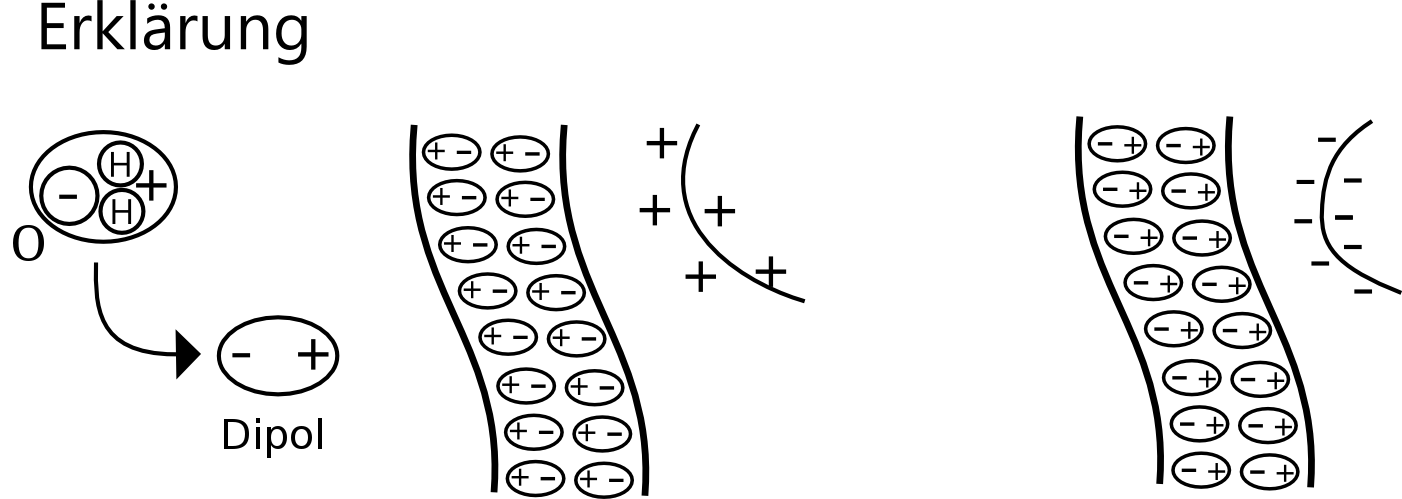
Ein Teilchen heiþt Dipol, wenn es zwar insgesamt neutral geladen ist, die Ladungen in ihm aber so verteilt sind, dass es zwei Pole besitzt.
12.: Induzierte Dipole
Exp.: Auf einem Tisch liegende Grieskˆrner werden sowohl von einer negativ geladenen, als auch von einer positiv geladenen Folie angezogen.
Erkl‰rung: Durch die Influenz verr¸cken die in den Grieskˆrnern fest sitzenden Ladungen etwas, wodurch kleine Dipole entstehen.
13.: Faraday's Feldtheorie
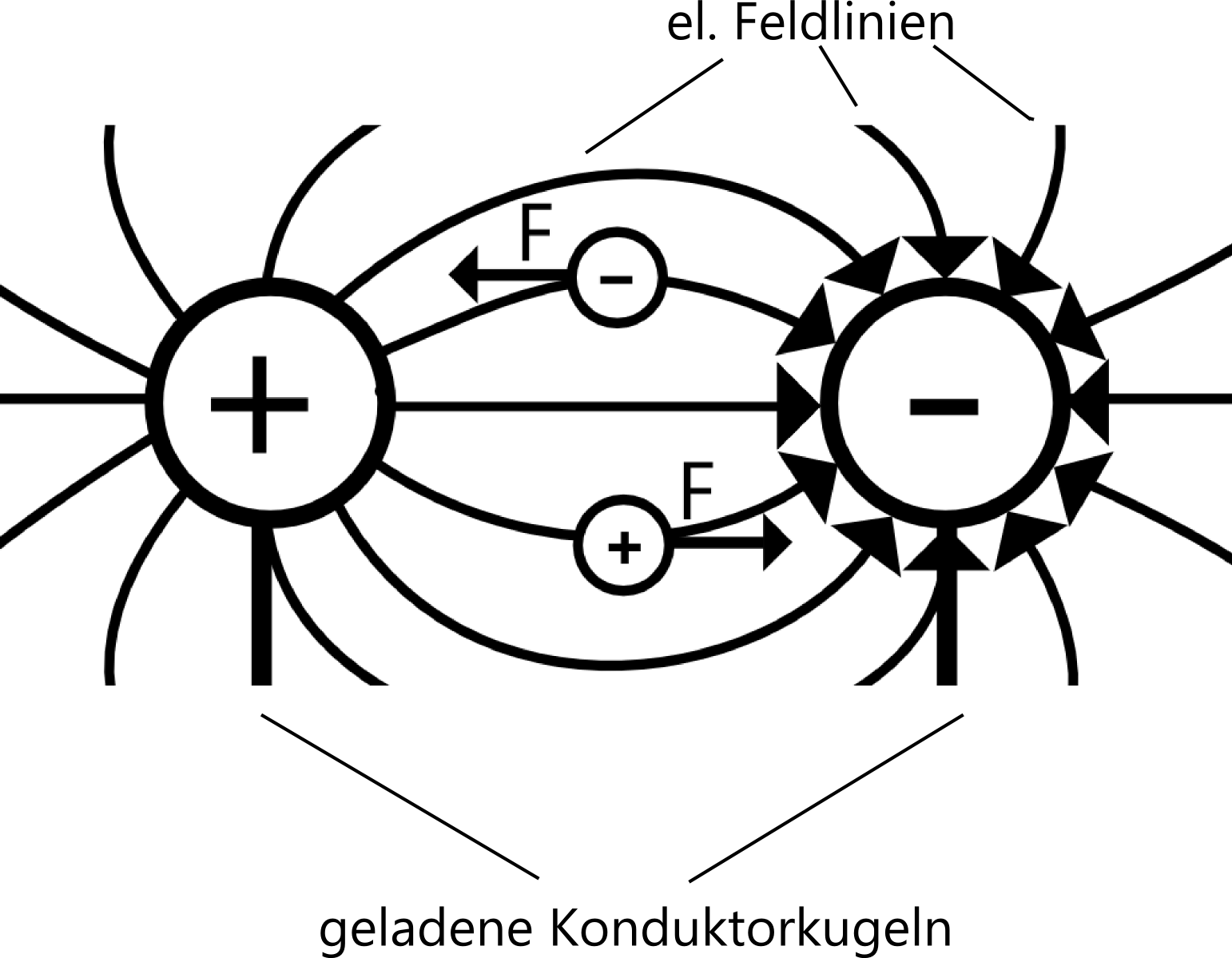
Wie zieht eine Ladung eine andere zu sich her oder stˆþt sie ab?
- Fr¸her glaubte man an Fernkr‰fte
- Faraday nahm das Umfeld von Ladungen durch ein elektrisches Feld durchzogen an, welches die elektrischen Kr‰fte bewirkt.
- Ladungen erfahren in elektrischen Feldern Kr‰fte, die tangential zu den Feldlinien wirken.
14.:Feldlinienbilder von Punktladungen und Kondensatoren
Experiment: Mit Grieskˆrnern in einer Schale mit Rizinus-÷l wird folgendes untersucht:
Das Feld einer Punktladung:

Das Feld zweier sich anziehender Punktladungen:

Das Feld zweier sich abstoþender Punktladungen:

Das Feld eines Kondensators:
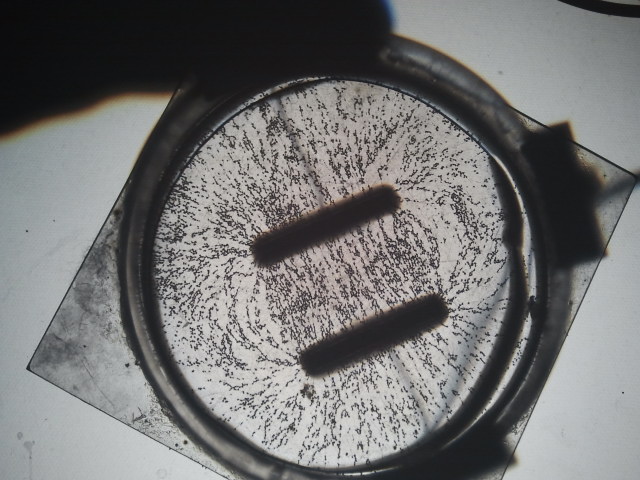
Zwischen zwei Kondensatorplatten verlaufen die Feldlinien parallel und im gleichen Abstand. Ðberall ist die St‰rke des elektrischen Feldes gleich groþ. Solche Felder nennt man homogen.
15.: Elektrische Kr‰fte wirken tangential zu den Feldlinien
Experiment: Eine kleine gelandene Konduktorkugel wird an einem Faden in den Kondensator gehalten
Beobachtung: Die Kugel schkl‰gt parallel zur E-Feld-Richtung aus, wenn sie positiv gelanden ist. Bei negativer Ladung schl‰gt sie antiparallel zur E-Feld-Richtung aus.
=> die Kr‰fte wirken tangential zu den Feldlinien (F II E-Feld)

16.: Die Feldlinien enden senkrecht an der Oberfl‰che geladener metallischer Kˆrper
(siehe Arbeitsblatt)
17.: Der Faraday'sche K‰fig
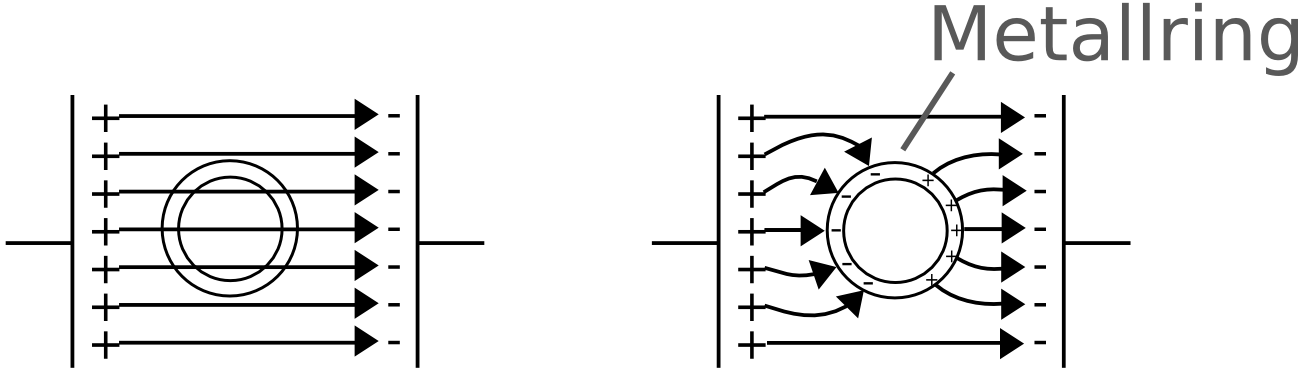
=> Aufgrund der freien Beweglichkeit der Ladungen, bewegen sich diese so lange, bis das Feld im Inneren ausgeglichen ist.
18.: Der Zusammmenhang zwischen Ladung, Kraft und St‰rke des E-Feldes
Wovon h‰ngt die Str‰ke der auf die Ladung q wirkende Kraft ab?
=>q, E:
- Je grˆþer q, desto grˆþer F
- Je grˆþer E, desto grˆþer F
=> Definitionsgleichung f¸r E:
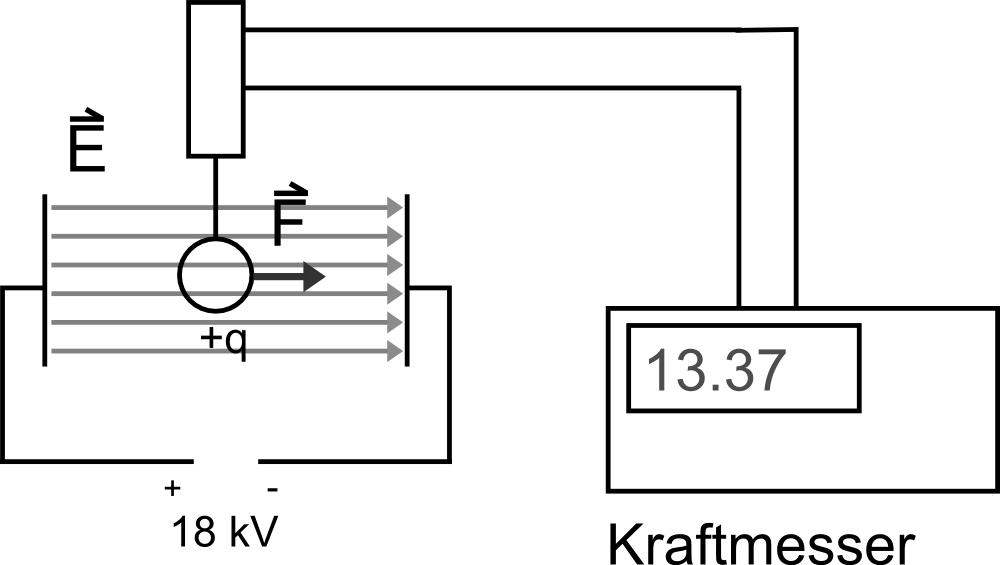
19.: Parallelen und Unterschiede zwischen elektrischem Feld und Gravitation

Analogien:
| Feldart | gravitativ | elektrisch |
|---|---|---|
| Eigenschaft des Probekˆrpers | Masse m | Ladung |
| Kr‰fte | ||
| Feldst‰rke | ||
| Arbeit bei Strecke d parallel zum Feld | => im homogenen Feld |
Unterschiede:
=> Gravtiationsfeld wirkt an Masse, E-Feld auf Ladungen
=> Gravitationskr‰fte wirken nur anziehend, E-Kr‰fte kˆnnen zudem abstoþend wirken
=> Es gibt nur eine "Art" masse der zwei "Arten" Ladungen
20.: Bewegungen senkrecht und diagonal zu den Feldlinien
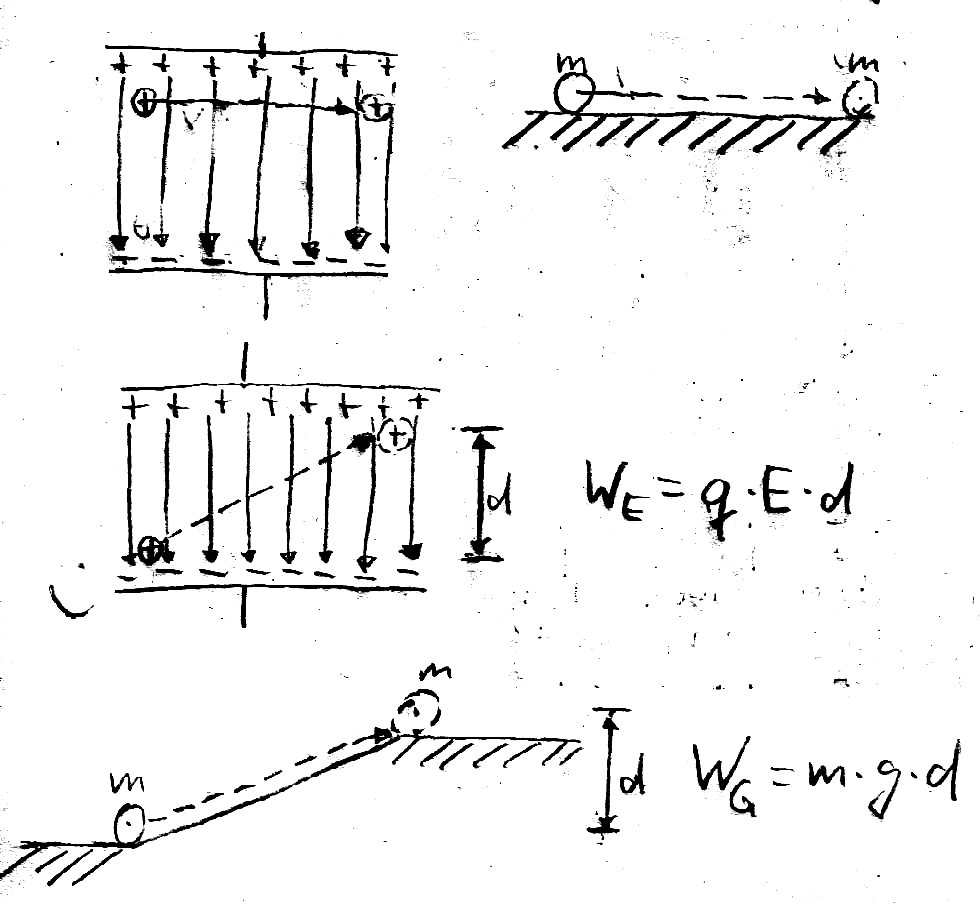
1. Bildreihe: Wie bei der Gravitation bei Massen auch, wird keine Arbeit durch das Feld verrichtet wenn sich die Ladungen senkrecht zu den Feldlinien bewegen.
2+3 Bildreihe: Wie bei der Gravitation h‰ngt die Transportarbeit nur von dem Anteil "d" der Strecke ab, der in Richtung der Feldkr‰fte verl‰uft.
21.: Definition der Spannung
Feldlinien verrichten an der Ladung "q" zwischen zwei Punkten die Transportarbeit "W". Die elektrische Spannung zwischen diesen Punkten ist dann wie folgt definiert:
=> Spannung = Verrichtete Arbeit / Ladung
Einheit:
Die Spannung 1V bedeutet also, dass beim Transport der Ladung 1C von den Feldkr‰ften die Arbeit 1J verrichtet wird.
22.: Untersuchung der Spannung zwischen Kondensatorplatten
Exp.: Zwischen zwei Aluminiumstreifen, welche die Kondesatorplatten darstellen, wird ein feuchtes Papiertuch gelegt. Die "Platten" werden mit einem Netzger‰t auf die Spannung 9 Volt gebracht. Das Ganze wird zur Abschirmung von auþen auf eine Styroporplatte gelegt. Mit einem Messverst‰rker kˆnnen nun die Spannungsdifferenzen zwischen zwei beliebigen Punkten zwischen den Platten gemessen werden.
Feststellungen:
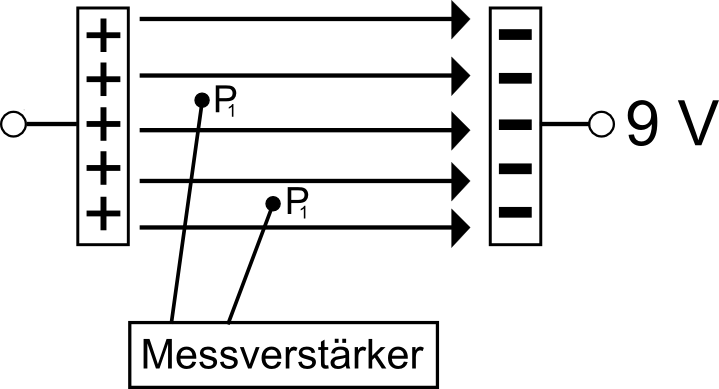 -Zwischen zwei Punkten, die auf einer Parallelen zu den Kondensatorplatten liegen, ist die Spannung
-Zwischen zwei Punkten, die auf einer Parallelen zu den Kondensatorplatten liegen, ist die Spannung
-Die Spannung nimmt parallel zu den Feldlienien linear zu.
=>Spannung existiertin einem Feld auch wenn keine Ladungen transportiert werden. Sie gibt die Arbeit pro Ladung an, die ein Feld verrichten w¸rde, wenn sich die Ladung von dem einen zum anderen Punkt bewegt.
23.:Potential und ƒquipotentialfl‰che
In Anlehnung an die potentielle Energie aus der Mechanik, nennt man die Spannung relativ zur zu einem festen Bezugspunkt (z.B. linke Kondensatorplatte), welcher einfach willk¸rklich festgelegt werden kann, Potential.
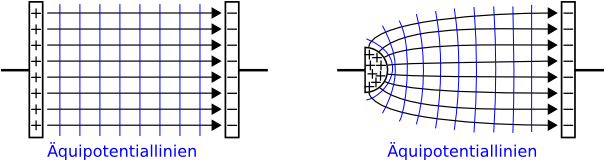
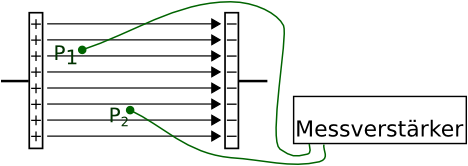
Punkte aus 22., zwischen denen die Spannung 0 ist, liegen auf einer Parallelen zu den Kondesatorplatten. Auf allen Punkten dieser Parallelen h‰tte die Ladung die selbe "elektrische potentielle Energie" bzw. das selbe Potential, da keine Arbeit verrichtet werden muss, um sie von einem Punkt zu einem anderen entlang einer dieser Lienien zu verschieben. Man nennt die Parallele daher ƒquipotentialfl‰che.
24.: Der Zusammenhand zwischen U, E und d beim Plattenkondensator
Der Abstand zweier Kondensatorplatten ist d. Diese sind an der Gleichspannung U angeschlossen und werden von dieser Spannungsquelle geladen. Darin verrichtet das Feld auf eine Probeladung q, die von einer Platte zur anderen transportiert wird, die Arbeit
. Daraus folgt f¸r die Spannung zwischen den Platten:- Experimentelle Ðberpr¸fung
D.h. ¸ber die an einem Plattenkondensator anliegende Spannung l‰sst sich eine Aussage ¸ber die St‰rke des E-Feldes machen.
25. Die Elektronenkanone
Ladung:
Masse: Sp‰ter wird gezeigt, wie man dies experiementell ermittelt.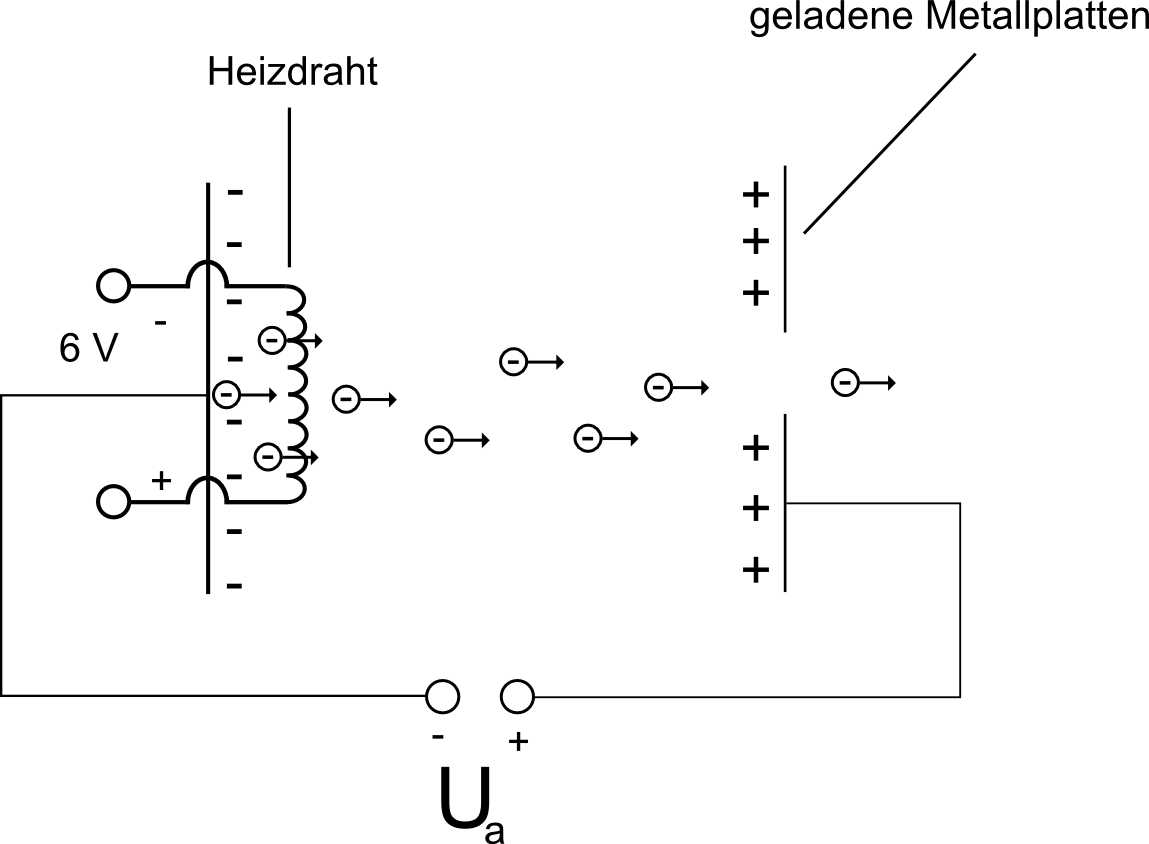
Die Idee:
- Ðber einen Gl¸hdraht Eletronen auslˆsen
- Im elektrischen Feld zweier Kondensatorplatten die Elektronen beschleunigen
- Die Elektronen durch eine L¸cke in der hinteren Platte rausfliegen lassen
Berechnung der Geschwindigkeit der Elektronen:
Exp.: Die Elektronen in einem Experiment werden mit 5000V beschleunigt. Wie groþ ist ihre Geschwindigkeit?
Hinweis: Bei noch hˆheren Beschleunigungsspannungen muss relativistisch gerechnet werden.
26. Die Einheit Elektronenvolt
Ein Elektronenvolt (kurz: eV) ist die Arbeit, die ein elektrisches Feld an der Ladung 1e verrichtet, wenn diese von einem Punkt zu einem anderen Punkt mit der Spannung 1V zwischen diesen beiden Punkten bewegt wird. Durchl‰uft ein Teilchen der Ladung 1e die Spannung, so erhˆht sich seine kinetische Energie um 1eV.
27.: Das Ablenksystem einer Brownischen Rˆhre
Die Elektronenkanone aus Aufgabe 25 erzeugt sogenannte Elektronenstrahlen, die auch Kathodenstrahlen genannt werden. In alten Fernsehrger‰ten leuchten diese Kathodenstrahlen die Mattscheibe aus, indem sie sehr schnell zeilenfˆrmig von links oben nach rechts unten gelenkt wurden und auf der Scheibe an der jeweiligen Position einen Punkt zum Leuchten brachten. Heute findet die Ablenkung der Sttrahlen noch in Elektroskopen Anwendung. Doch wie kˆnnte man solche Kathodenstrahlen ablenken?
Exp: Ein Kathodenstrahl wird von einem homogenen el. Feld abgelenkt.
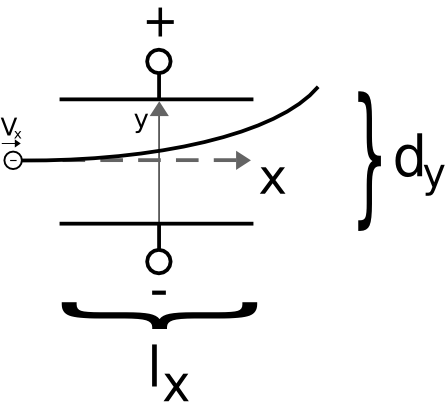
Flugbahnberechnung:
- Die Elektronen wurden durch die Beschleunigungsspannung Ua auf die Geschwindigkeit in x-Richtung
- Wegen der Platten wirkt in y-Richtung die Kraft
- Diese beschleunigt die Elektronen gem‰þ
=>
- In x-Richtung legen die Elektronen in der Zeit t die Strecke zur¸ck. F¸r die Breite der Platten benˆtigen sie daher die Zeit .
- W‰hrend dieser Zeit beschleunigen sie mit ay. Sie erreichen nach der Zeit tp die Geschwindigkeit in y-Richtung:
- Am Ende der Kondensatorplatten haben die Elektronen dann den folgenden Weg in y-Richtung zur¸ckgelegt:
=>Der Verlauf des Kathodenstrahls in y-Richtung ist unabh‰ngig von Masse und Ladung der Ladungstr‰ger.
28. Ziel: Der Zusammenhang zwischen Fl‰chenladung und Feldst‰rke

Experiment: Eine Metallscheibe mit dem Radius r= 0,05m wird an die Innenfl‰che einer Kondensatorscheibe gedr¸ckt. Die auf dieser Fl‰che befindlichen Ladungen werden mit der Scheibe abgehoben. Die auf der Scheibe befindliche Ladung wird gemessen.
Wovon h‰ngt es ab, wie viel Ladung auf die Scheibe passt?
- Je grˆþer die Spannung U, desto grˆþer die Ladung Q (d konstant) - Je grˆþer der Abstand d, desto kleiner die Ladung Q (U konstant)
Durchf¸hrung des Experiments, Meþwerte:
| Spannung U | Abstand d | Feldst‰rke E = U/d | Ladung auf Scheibe Q | Q |
| 2500 V | 4 cm | 62500 V/m | 4,7 nC | 5,89 * 10^-7 |
| 4000 V | 4 cm | 1000000 V/m | 7,1 nC | 9,04 * 10^-7 |
| 5500 V | 4 cm | 137500 V/m | 9,5 nC | 1,2 * 10^-6 |
| 2500 V | 2 cm | 125000 V/m | 9,5 nC | 1,2 * 10^-6 |
| 2500 V | 6 cm | 41666,7 V/m | 2,8 nC | 3,57 * 10^-7 |
| 4000 V | 6 cm | 66666,7 V/m | 4,1 nC | 5,22 * 10^-7 |
| 5500 V | 6 cm | 91666,7 V/m | 5,4 nC | 6,88 * 10^-7 |
| 10000V | 6 cm | 166666,7 V/m | 11,1 nC | 1,41 * 10^-6 |
Ergebnis: Unabh‰ngig von U oder d ist Q immer proportional zu E.
29. Die Fl‰chenladung h‰ngt tats‰chlich nur vom Feld E ab!!
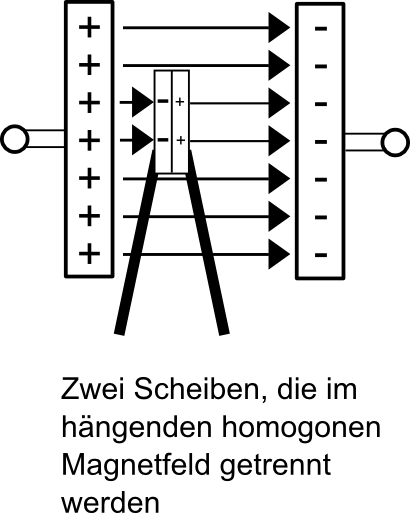
Zwei Scheiben werden im homogenen Feld E senkrecht zu den Feldlinien zusammen gehalten. Wegen Influenz kommt es zu der in der Abbildung gezeigten Ladungstrennung. Die Scheiben werden im Feld getrennt und die Ladungen gemessen. Ergebnis: Auf den Scheiben ist genau so viel Ladung wie auf einer gleich groþen Fl‰che der Kondensatorplatten.
- Da an den Scheiben keine Spannung anliegt, sondern diese nur mit dem E-Feld wechselwirken, folgt: Die Menge an Ladungen h‰ngt nur von der St‰rke des elektrischen Feldes ab.
30. Die Fl‰chenladungsdichte
Die Fl‰chenladungsdichte ist ein Maþ daf¸r, wie dicht die Ladungen auf einer Fl‰che sitzen
Einheit: c/m≤W‰hrend due Ladungsmenge auf einer Platte von ihrer "Grˆþe" abh‰ngt, ist die Flachenladungsdichte von der dieser Grˆþe unabh‰ngig. Bei gleicher Fl‰che gilt:
-> Je grˆþer die Fl‰chenladungsadichte, desto grˆþer die Ladung Q.
31. Der Zusammenhang zwischen Fl‰chenladungsdichte und Feldst‰rke
Experiment Nr. 28 zeigt, dass die Ladung auf einer Scheibe proportional zur Feldst‰rke steigt. Da die Fl‰che konstant bleibt, steigt auch die Fl‰chenladungsdichte proportional zur Feldst‰rke E, wie man aus der Tabelle Nr. 28 erkennen kann.
Der Proportionalt‰tsfaktor
heiþt "elektrische Feldkonstante". Sie kann mit den Werten aus Nr. 28 berechnet werden.32. Die Kapazit‰t eines Kondensators
Wie viele Ladungen passen auf einen Plattenkondensator?
Von der Grˆþe
h‰ngt es ab, wie viele Ladungen bei fester Spannung auf den Kondensator passt. Sie heiþt deshalb auch Kapazit‰t des Kondensators C. Einheit: Eine Kapazit‰t von 1 Farad bedeutet,dass der Kondensator bei einer Spannung von 1V die Ladung 1C speichert. Wann wird die Kapazit‰t mˆglichst groþ? =>Wenn A mˆglichst groþ und d mˆglichst klein wird.33. Dieelektrizit‰tszahl
Exp._ Durch
wird die Kapazit‰t eines Plattenkondensators bestimmt. Anschlieþend wird eine Plexiglasscheibe zwischen die Kondensatorplatten eingeschoben und der Vorgang wiederholt: (Spannung gleich) Durch die Plexiglasscheibe hat sich die Kapazit‰t um den Faktor erhˆht. Diese Zahl ist vom eingeschobenen Stoff abh‰ngig und wird Dielektrizit‰tszahl genannt.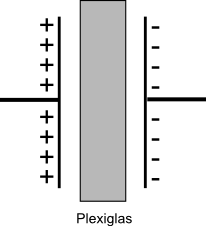
| Stoff | Dielektrozitˆtszahl |
| Luft | 1,00058 |
| Wachs | 2 |
| Glas | 5 bis 16 |
| Alkohol | 26 |
| Wasser | 81 |
| Keramik mit BgSr | 10000 |
Daraus folgt f¸r die Kapazit‰t eines Kondensators und seine Fl‰chenladungsdichte:
34. Mikroskopische Betrachtung von Isolatoren in elektrischen Feldern
Weshalb erhˆht sich die Kapazit‰t eines Plattenkondensators, wenn man in sein Feld einen Plattenkondensator schiebt?
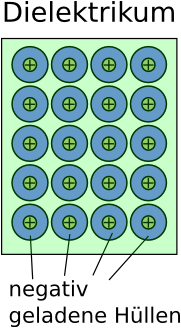
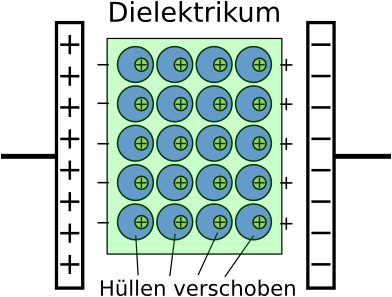
Die Atome der Isolatoren bestehen aus einem positiv geladenen Kern (+) und einer negativ geladenen H¸lle um den Kern herum (grau schraffiert). Zwar sind die Elektronen der H¸lle an ihre Atome gebunden, allerdings verschieben sich die Elektronenwolken leicht zur positiven Platte. Dadurch wird die in der Abbildung linke Isolatorseite negativ, die rechte positiv geladen. Diese Ladungen ziehen zus‰tzliche Ladungen auf die Platten. Das durch die Polarisationsladungen des Isolators entstehende innere Feld schw‰cht im Isolator das durch den Kondensator verursachte Feld ab.
35. Parallelschaltung von Kondensatoren
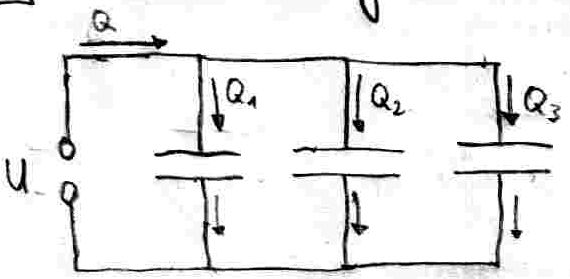
Liegt an n parallel geschalteten Kondensatoren die Spannung U an, so entspricht die Gesamtladung der Summe der Einzelladungen.
Wollte man diese Kondensatoren durch einen einzigen "Ersatzkondensator" ersetzen, so m¸sste dieser also die folgende Kapazit‰t haben:
Die Ersatzkapazit‰t von parallel geschalteten Kondensatoren ist somit die Summe der Einzelkapazit‰ten.
36. Reihenschaltung von Kondensatoren - Betrachtung der Einzelspannungen
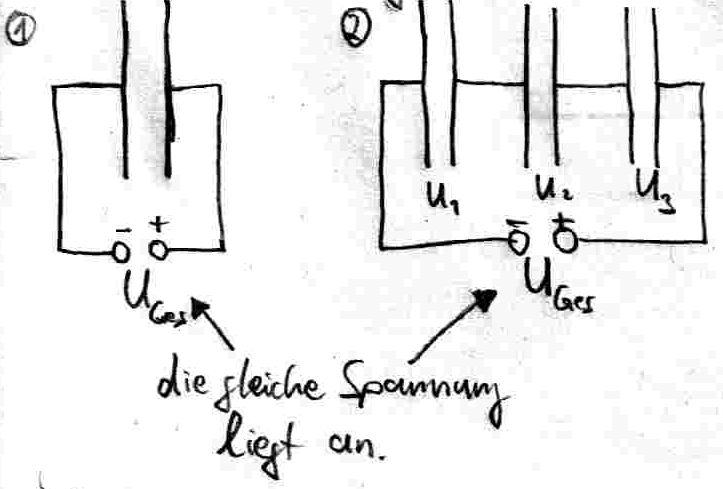
Bei 1 wird beim Transport der Ladung q von der einen Platte zur anderen die Arbeit
verrichtet. Die gleiche Arbeit muss wegen der gleich groþen Spannung verrichtet werden, wenn bei 2 eine gleich groþe Ladung z.B. von der linken Platte des linken Kondensators ¸ber den mittleren Kondensator zur rechten Platte des rechten Kondensators transportiert wird. F¸r die einzelnen Transportarbeiten der drei Platten gilt demnach:
Betrachtet man die Spannung als Arbeit pro Ladung, so erh‰lt man:
Allgemein gilt bei n Kondensatoren:
--> Hier fehlt noch Text!
37.Reihenschaltung von Kondensatoren - Betrachtung der Ersatzkapazit‰t}
Welche Kapazit‰t m¸sste ein Ersatzkondensator haben, der n parallel geschaltete Kondesatoren mit den Kapazit‰ten
ersetzt?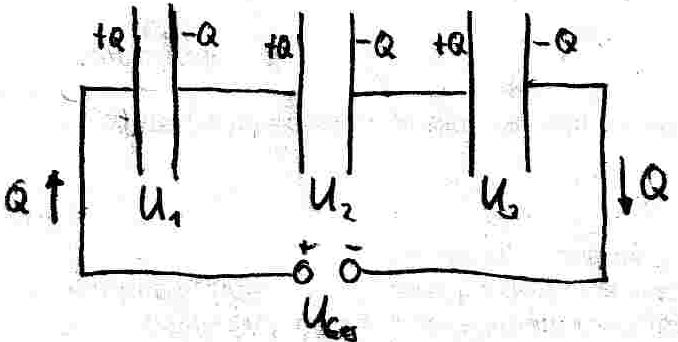
Entzieht das Netzger‰t der Platten ganz links Elektronen, so wird sie positiv (+Q) geladen. Aufgrund von Influenzen werden wegen der positiv geladenen linken Platte Elektronen auf die Platte gegen¸ber gezogen, wodurch sie die gleichgroþe negative Ladung -Q tr‰gt. Die Elektronen kommen von der linken Platte des Nachbarkondensators, welcher die gleiche positive Ladung +Q tr‰gt wie die Platte ganz links. Und so weiter.
-> Jeder Kondensator enth‰lt die gleiche Ladungsmenge.
Wegen der sich unterscheidenden Kapazit‰ten sind damit aber die Teilspannungen unterschiedlich:
Bei einer Reihenschaltung von Kondesatoren entspricht der Kehrwert der Ersatzkapazit‰t dem Kehrwert der Einzelkapazit‰ten.
38. Die SI-Grundeinheiten}
Die SI-Grundeinheiten wurden wie folgt festgelegt:
Meter (m), Sekunde (s), Kilogramm (kg), Ampere (A)
Alle Einheiten lassen sich aus diesen Grundeinheiten zusammensetzen:
->Kraft: Wegen
->Energie: Wegen ist
->Ladung: Wegen (sp‰ter mehr) ist
->Spannung: Wegen ist
->Kapazit‰t: Wegen ist
39. Das elektrische Feld einer Punktladung
Punktladungen kommen ¸berall in unserer Welt vor, z.B. Atomkerne oder Elektronen. Wir untersuchen jetzt aber das Feld, welches die Elektronen auf ihren Bahnen um die Atomkerne h‰lt.
Aus dem Versuch mit Grieþkˆrnern wissen wir, dass die Feldlinien radial nach auþen gehen. Doch wie kann man die St‰rke des Feldes im Abstand r von der Punktladung Q berechnen?
->Beim Verdoppeln der Ladung Q verdoppelt sich auch die Anzahl der Feldlinien. Die Feldst‰rke um Q ist also wahrscheinlich proportional zu Q.
->Die Oberfl‰che einer Kugel vervierfacht sich wegen
=> wobei k ein Proportionalit‰tsfaktor ist.
40. Die Coulomb-Kraft
Die Zentralladung q1 verursacht das elektrische Feld
Welche elektrische Kraft wirkt zwischen ihr und einer zweiten Ladung q2?Diese Kraft zweier Zentralladungen im Abstand r zueinander nennt man Coulomb-Kraft.
41. Vergleich der Coulombkraft mit der Gravitationskraft
42. Transportarbeit zwischen 2 Punkten im Coulomb-Feld
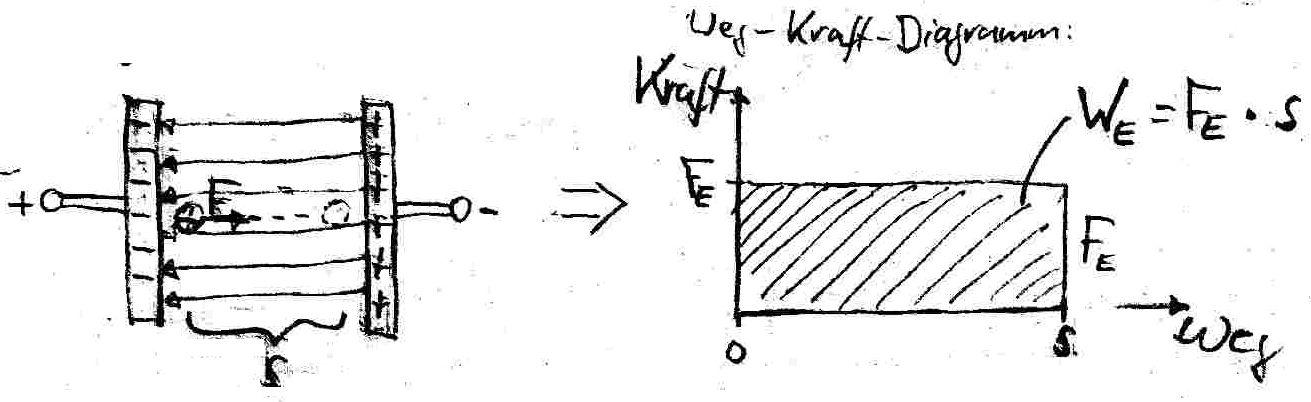
Die Transportarbeit entspricht der Fl‰che im s-F-Diagramm.
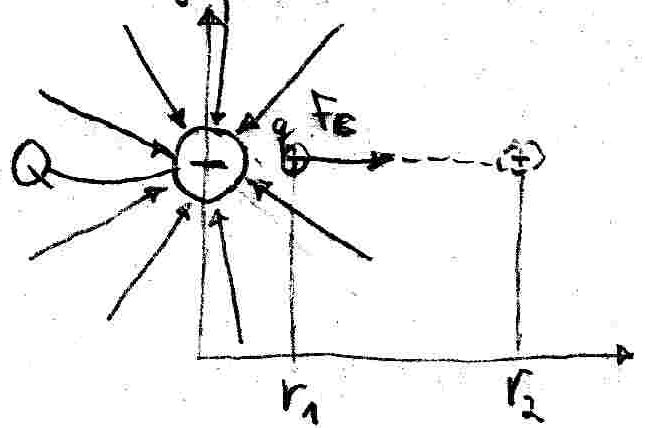
Problem:
ist nicht mˆglch, da die Kraft F_E nicht konstant ist: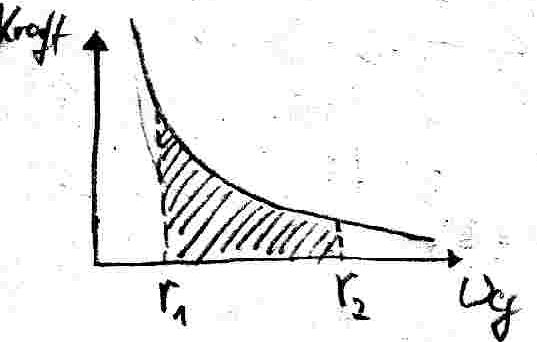
Vermutung:
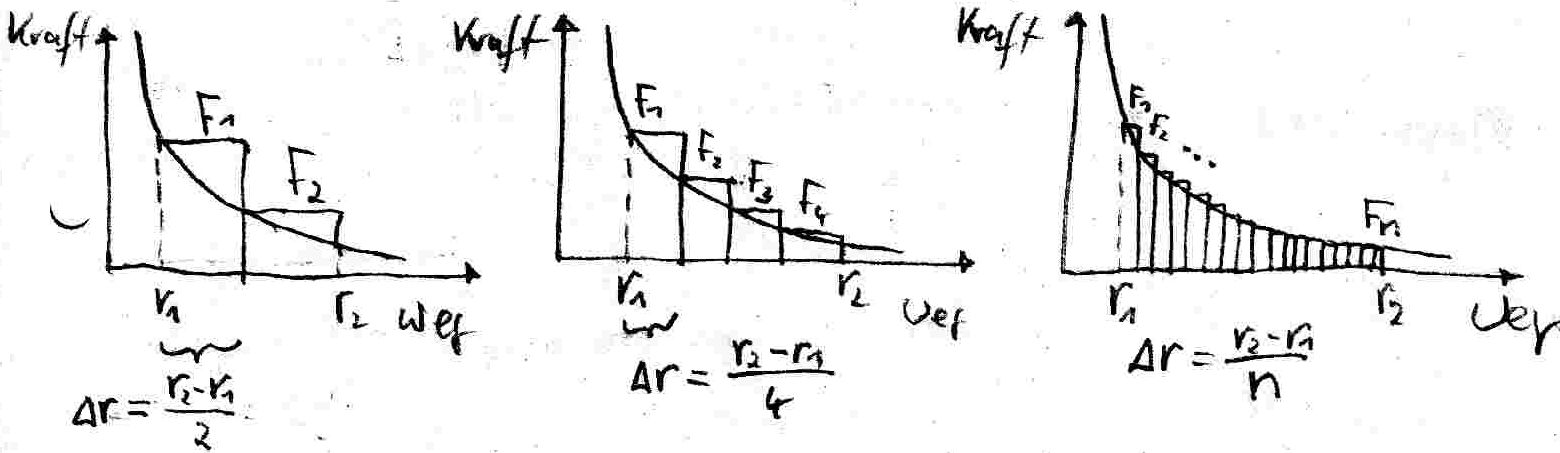
F¸r eine Einteilung in unendlich viele, unendlich schmale Rechtecke gilt offenbar:
f¸r mitDie Mathematiker schreiben das so:
mit dr=infinitesimu(kleines)Mithilfe der Integralrechnung erhalten wir:
43. Spannung zwischen 2 Punkten im Coulomb-Feld Die Spannung ist definiert als
F¸r die Spannung zwischen zwei Punkten im Coulomb-Feld, die den Abstand r_1 bzw r_2 von der Zentralladung Q entfernt liegen folgt:44 Das Coulomb- Potential
Als Coulomb- Potenzial bezeichnet man die Spannung relativ zu einem unendlich weit entferneten Punkt im Feld einer Zentralladung:
F¸r r_2 -> ∞ l‰uft 1/r_2 -> 0
Damit folgt f¸r das Potential eines Punktes mit Abstand r_1 zur Zentralladung Q
Wegen
und folgt f¸r die Kapazit‰t einer Kugel:46. Potential zweier mit Polen verbundenen Dr‰hte
Der Versuchsaufbau:
Wir verbinden zwei Drahtst¸cke mit unterschiedlichen Polen einer Spannungsquelle. Die beiden Spitzen der Dr‰hte sind sich sehr nahe, ber¸hren sich jedoch nicht.
Es w‰re ein normaler kleiner Stromkreislauf, wenn sich die Spitzen ber¸hren w¸rden.

Wie man auf der Skizze bereits sehen kann, bildet sich ein Feld zwischen den beiden Drahtspitzen.
Aus folgendem Grund:
Die Spannungsquelle entzieht dem Draht am positiven Pol Elektronen und 'pumpt' diese auf den Draht am negativen Pol.
Dadurch laden sich die Dr‰hte unterschiedlich und an der Spitze entsteht ein elektrisches Feld.
Potential ist die Spannung zwischen zwei Punkten zu einem (willk¸rlich festgelegten) Nullpunkt.
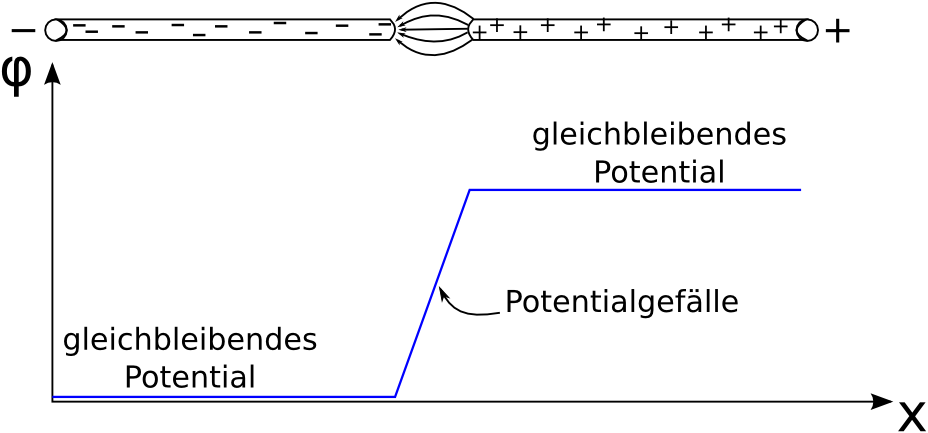
Das elektrische Feld stellt sich als 'Potentialgef‰lle' zwischen den beiden unterschiedlich geladenen Dr‰hten heraus. Diese Erfahrung haben wir auch schon bei Untersuchungen mit 2 Plattenkondensatoren gemacht.
StromBedeutung? 47. Qualitative Bedeutung des elektrischen Stroms
F¸hrt man nun die beiden Drahtenden aus 46. zusammen so bekommen die Elektronen die Mˆglichkeit durch beide Drahtst¸cke hindurchzuflieþen, vom einen zum anderen Pol. Ein Kurzschluss gewissermaþen.
F¸r das Potential bedeutet das, dass es kein Gef‰lle mehr DURCH das Feld geben kann. Das Feld hat sich bei der Zusammenf¸hrung der beiden Drahtenden aufgelˆst. Trotzdem gibt es an der Stromquelle eine Potentialdifferenz zwischen dem positiven und dem negativen Pol.
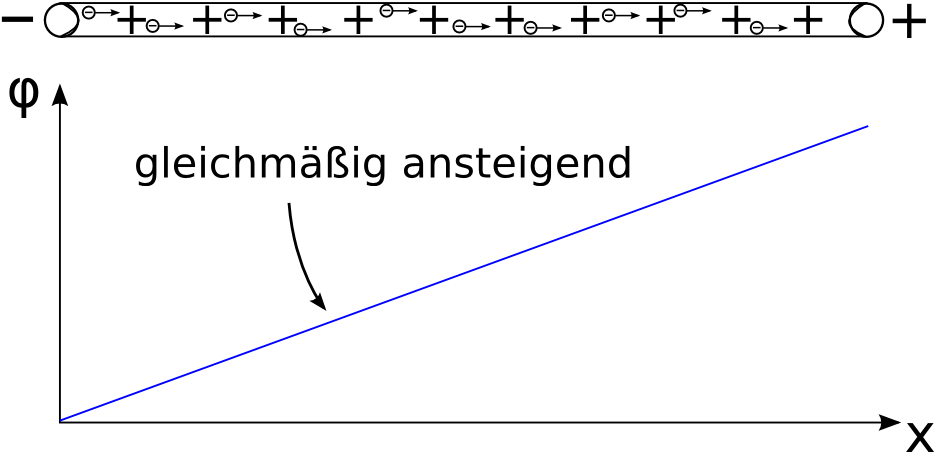
Anscheinend steigt das Potential ¸ber den kompletten Draht gleichm‰þig linear.
Die flieþenden Elektronen stoþen dabei st‰ndig mit Atomr¸mpfen zusammen. Ein Teil ihrer Arbeit W = U * q wird dabei in W‰rmeenergie umgewandelt.
Dadurch erhˆht sich die Temperatur des gesamten Drahtes nach einer Weile f‰ngt er an zu gl¸hen.
Es gilt:
Flieþt die Ladung q ¸ber den Draht wird die Energiemenge U * q in W‰rmeenergie umgewandelt.
48. Die elektrische Stromst‰rke
F¸r die durchschnittliche Stromst‰rke im Zeitraum
gilt Bei konstanter Stromst‰rke kann diese Formel immer verwendet werden. F¸r die momentane Stromst‰rke gilt: Einheit: 1 Ampere = 1Coulomb / 1Sekunde49. Begriff der elektrischen Leistung Eine Lampe wird an eine Stromquelle mit U = 6V angeschlossen. Es wird ein Strom um 0,5 A gemessen! Wie viel elektrische Energie wird an der Lampe in W‰rme- und Lichtenergie umgewandelt?
- 0.5A bedeutes ist flieþt in 1s die Ladung -0,5C von - nach +
- Damit verrichtet das Feld in jeder Sekunde die Arbeit W_{E}=U*Q, also in jeder Sekunde
- nach der Zeit wird die Arbeit verrichtet
Definition: Die Arbeit, die pro Zeit verrichtet wird, nennen wir Leistung
Einheit: 1Watt=1Joule/1SekundeLeistet eine Gl¸hlampe 60 Watt, so bedeutet dies, dass sie in jeder Sekunde 60 Joule elektrische Energie in W‰rme- und Lichtenergie umwandelt.
50.Berechnung der Leistung
In einer Gl¸hbirne wird in der Zeitspanne Δt die Arbeit ΔW
verrichtet. F¸r die Leistung gilt somit wegen :BSP.: Leistung einer Lampe, eines Fˆns, Laptops,... bestimmen.
51. Die Einheit Kilowattstunden
Eine Kilowattstunde (kurz 1kWh) entspricht der Arbeit,die bei einer Leistung von 1000 Watt in einer Stunde verrichtet wird.
1kWh = 1000 Watt*3600 Sekunden = 3600000 Joule = 3,6 Mio. Joule
In Kraftwerken erzeugt man die elektrische Energie 1kWh aus 0,3kg Steinkohle; 1,5kg Braunkohle; 4m^3 Wasser bei 100m Hˆhenunterschied oder 0,05mg Uran 235 im Kernkraftwerk.
52. Der elektrische Widerstand
Experiment: Ðber einen dicken Draht und eine dahinter geschaltete Gl¸hbirne flieþt ein Strom, die Gl¸hbirne leuchtet hell. Anschlieþend wird der dicke Draht durch einen d¸nnen ausgetauscht. Ergebnis: Die Gl¸hbirne leuchtet dunkler...was ist passiert???
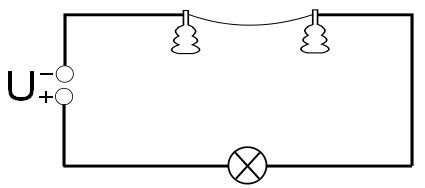
=> Der Ladungsstrom hat offenbar grˆþere Schwierigkeiten, durch den d¸nnen Draht zu flieþen als durch den dicken => In der Physik sagt man: Der elektrische Widerstand des d¸nnen Drahtes ist grˆþer als der des dicken => Erhˆht man die anliegende Spannung, so flieþt auch mehr Strom durch den Draht. Aufgrund des dadurch st‰rkeren elektrischen Feldes im Leiter, werden die Elektronen mit einer grˆþeren Kraft durch den Stromkreis gezogen
Je-desto-Beziehungen: => Je grˆþer der Strom bei gleichbleibender Spannung, desto kleiner der Widerstand => Je grˆþer die Spannung bei gleichbleibendem Strom, desto grˆþer der Widerstand
- R=U/I erf¸llt die Beziehungen und eignet sich als Definition f¸r den Widerstand
Das Ohm'sche Gesetz:
Widerstand = Anliegende Spannung / Durchflieþenden StromEinheit: 1
= 1V/1A 1Ohm = 1Volt/ 1AmpereBeispiele: Wir messen den Widerstand... ...einer Gl¸hbirne ...eines Fˆhns ...eines Tauchsieders
53. Reihenschaltung von Widerst‰nden
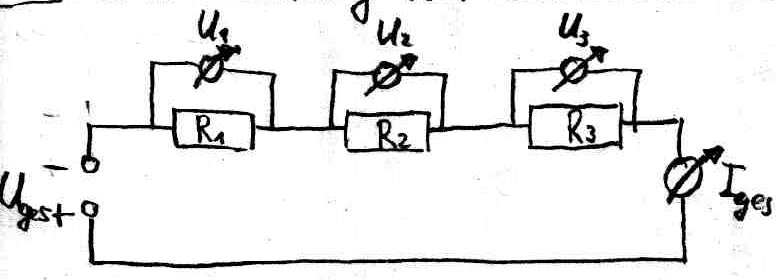
Bei einer Reihenschaltung durchl‰uft der Strom nacheinander alle in Reihe geschalteten Widerst‰nde.
Es gelten folgende Gesetze bei n in Reihe geschalteten Widerst‰nden:
<- wird auch "Ersatzwiderstand" genannt <- Durch den Widerstand flieþt der selbe Strom54. Parallelschaltung von Widerst‰nden
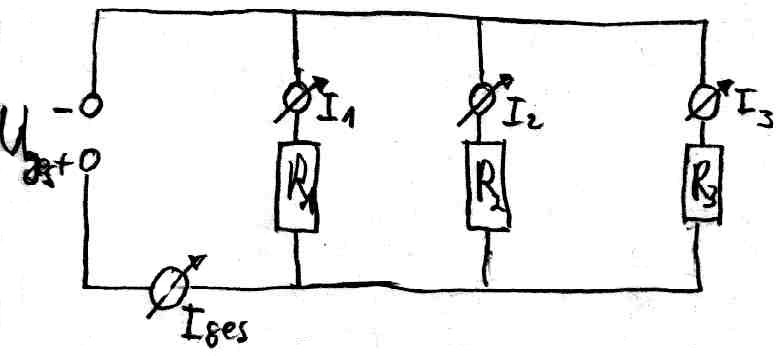
Bei einer Parallelschaltung wird jeder parallel geschaltete Widerstand von einem anderen Strom durchflossen
Gesetze f¸r parallel geschaltete Widerst‰nde:
Nach dem Ohmschen Gesetz gilt:
daraus folgt:55.: Die in Kondensatoren gespeicherte Energie
Br‰uchte man zum Laden eines Kondensators immer die gleiche Spannung U, kˆnnte man leicht ausrechnen, wie viel Energie auf ihn gespeichert w‰re, wenn man die Ladung Q auf ihn l‰dt:
Dies entspricht im Diagramm der Fl‰che unter Graphen.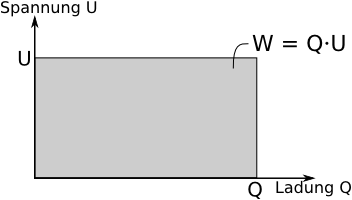
Allerdings benˆtigt man zum Laden eines Kondensators eine um so grˆþere Spannung, je mehr Ladung sich auf ihm befindet. Wegen
benˆtigt man die Spannung , die linear mit Q anw‰chst. Auch hier entspricht die zum Laden benˆtigte Arbeit der Fl‰che des Graphen im QU-Diagramm: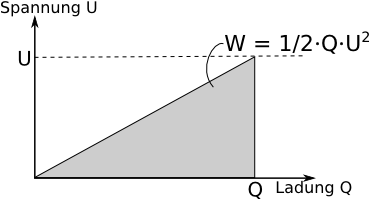
56. Die Energiedichte des elektrischen Feldes
Faraday ging davon aus, dass die Energie eines Kondensators im Feld des Kondensator gespeichert ist und somit den Zwischenraum zwischen den Platten durchsetzt:

mit dem vom Feld durchdr‰ngten Volumen V
Die Energiedichte des elektrischen Feldes gibt in diesem Zusammenhang an, wie viel Energie pro Volumeneinheit im Feld gespeichert ist:
57. Potential an Widerstand und Kondensator
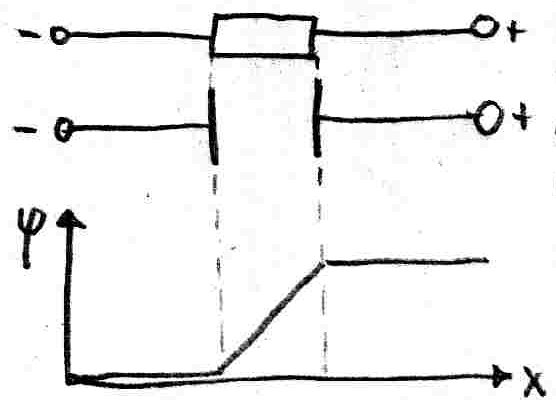
Das Potential entspricht der Spannung relativ zu einem Bezugspunkt. Wie aus der Abbildung deutlich wird, haben die Potentiale von Widerst‰nden und Plattenkondensatoren einen ‰hnlichen Verlauf. Unterschied: Beim Widerstand flieþen Ladungen. Damit verrichtet das el. Feld dort die Leistung
beim Kondensator nicht!58. Entladevorgang bei Kondensatoren
58.1 Potential bei der Kondensatorenentladung
Kondensatorenenladungen spielen nahezuin jedem Bereich der Technik eine Rolle. Insbesondere dort, wo sie als Energiespeicher dienen. Wir entladen den Kondensator ¸ber einen Widerstand R. Das Potential hat dabei folgende Form:
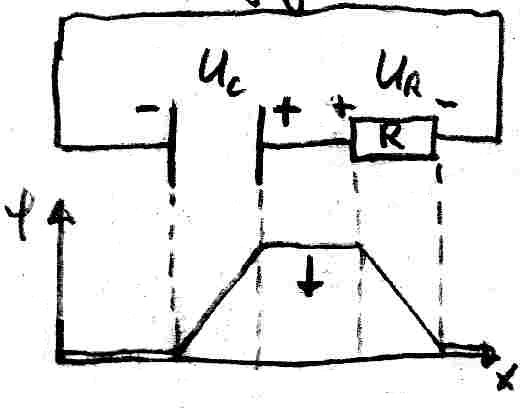
Die Ladungen fliþen dabei von der negativ geladenen Platte ¸ber den Wide4rstand zu positiv geladenen Platte. Dabei verliert der Kondensator an Ladung, womit seine Spannung sinkt. Damit f‰llt auch das Potential ab, was durch den Pfeil dargestellt wird.
58.2 Aufstellen einer Differentialgleichung
Da die Potentialdifferenz von links nach rechts beim Kondensator die gleiche ist, wie von rechts nach links beim Widerstand, gilt f¸r die anliegenden Spannungen U_C = -U_R Wir bringen diese Gleichung nun auf eine Form, die nur von den Kenngrˆþen C und R, sowie von der Ladung Q(t) auf dem Kondensator und ihrer ƒnderungsrate Q'(t) abh‰ngt.
Aus
wird damit==>
Dies ist eine Differentialgleichung (DGL). Q(t) ist eine Funktion, die angibt, wie viel Ladung nach der Zeit t noch auf dem Kondensator ist. Durch die DGL wissen wir: Setzt man Q(t) und seine Ableitung in die linke Seite der Gleichung ein, so muss Null herauskommen.58.3:
Experiment: Entladung eines Kondensators mit CASSY Durch die seitlich dargestellte Schaltung wird mit dem computergest¸tzten Messsystem CASSY der Strom- und Spannungsverlauf graphisch dargestellt.
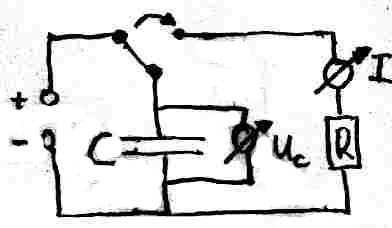
- Vermutlich f‰llt die Ladung Q(t) exponentiell ab
- Wir kˆnnen diese Vermutung pr¸fen, indem wir diese Funktionf¸r Q(t) in die DGL f¸r den Entladevorgeang einsetzen.
==> Offenbar ist die DGL nur erf¸llt, wenn wir
setzen.58.4 Entladefunktionen von Kondensatoren
Q_0 : Anfangsladung zum Zeitpunkt t=0
R : Widerstand, ¸ber den der Strom flieþt C : Kapazit‰t des Kondensatorsmit
U_0: Spannung am Kondensator zum Zeitpunkt t=0
=>
mit I_0 = (U_0)/R Anfangsstrom kurz nach Beginn der Entladung Der Strom ist negativ, weil die Ladung den Kondensator verlassen und Q(t) daher abnimmt.59.: Berechnung von Halbwertszeiten
Als Halbwertszeit bezeichnet man die Zeit, die beim Entladevorgang eines Kondensators verstreicht, bis nur noch die H‰lfte der Ladungen auf dem Kondensator sind. Mit der Funktion Q(t) ausgedr¸ckt gilt f¸r die Halbwertszeit t_h:
... nach Division durch Q_0 folgt:
Anwendung des Logarithmus Naturalis:
Und es folgt f¸r die Halbwertszeit t_h:
62.: Ferromagnetische Stoffe
Neben den Kr‰ften zwischen Magneten, ziehen Magneten auch andere Stoffe an. Diese sind Eisen(Fe), Kobalt(Co) und Nickel(Ni). Man nennt diese Stoffe deshalb ferromagnetische Stoffe*. Andere Stoffe werden von Magneten nicht angezogen.
"Ferro" kommt von der lateinischen Bezeichnung "Ferrum" f¸r Eisen. Ferromagnetische Stoffe haben also gleiche/‰hnliche Eigenschaften wie Eisen. Wie man sieht, sind Nickel und Kobalt ebenso magnetisierbar-genau wie Eisen.
Diese Stoffe lassen sich demnach auch magnetisieren, indem man sie immer in die selbe Richtung an einem Magneten vorbei reibt. Die im Kˆrper/Stoff enthaltenen Elementarmagneten orientieren sich an dem Magntet und richten sich geordnet aus. (Nordpol-S¸dpol-Nordpol-S¸dpol-Nordpol-.......S¸dpol). L‰sst sich ein Kˆrper leicht magnetisieren, bzw. lassen seine Elementarmagneten leicht ausrichten, so bezeichnet man diesen Stoff als magnetisch weich.
Allgemein gilt: Kˆrper, die von Magneten angezogen werden, sind auch selbst magnetisierbar.
Magneten verlieren ihre Magnetisierung durch der Verlust der Ausrichtung der Elementarmagneten. Dies geschieht durch:
- mechanische Ersch¸tterung
- Erhitzen (Curietemperatur: Stoff verliert magnetische Eigenschaften)
63. Separation der Pole eines Magneten
Exp.: Wir versuchen jetzt den Nordpol eines Magneten von seinem S¸dpol zu trennen. Dazu nehmen wir eine magnetisierte Eisennadel aus 62. und teilen sie mit einer Zange in zwei Teile.
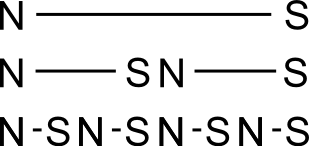
Ergebnis: Beide Teile haben nach wie vor Nord- und S¸dpol. Der Vorgang l‰sst sich beliebig oft wiederholen.
Wie lassen sich diese Effekte erkl‰ren? -> Modell Elementarmagnete
64. Modell der Elementarmagnete
Man stellt sich vor, dass aus vielen, sehr kleinen und nicht weiter teilbaren Magneten, den sogenannten Elementarmagneten, besteht. Mit dieser Vorstellung lassen sich alle Effekte der Magnetostatik erkl‰ren:

In nichtmagnetisierten Stoffen sind die Elementarmagnete ungeordnet und heben sich in ihrer magneteischen Wirkung auf. Der ferromagnetische Stoff als Ganzer nildet damit keine Pole aus.
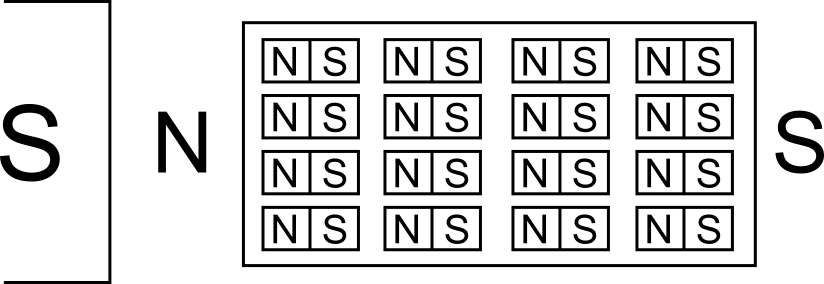
Streicht man den ferromagnetischen Stoff entlang einem Magneten, so richten sich die Elementarmagnete an den Polehn des Magneten aus und richten sich zum grˆþten Teil aus.Dadurch verst‰rken die Elementarmagnete ihre Wirkung und der ferromagnetische Stoff bildet selbst Pole aus.

Teilt man den magnetisierten Stoff, bleibt die Ausrichtung der Elementarmagnete bestehen. Beide Pole sind, wie in der Abbildung dargestellt, in beiden Bruchst¸cken vorhanden.
Durch Erhitzung oder starke mechanische Schl‰ge kann die Ordnung der Elementarmagnete wieder zerstˆrt werden. Der ferromagnetische Stoff hat dann seine Magnetisierung verloren. Er ist entmagnetisiert.
Wichtig ist: Es gibt keine magnetischen Monopole. Hierdurch unterscheiden sich Magnete von geladenen Kˆrpern: Magnete haben immer zugleich einen Nord- wie einen S¸dpol.
69. Kraft auf stromdurchflossene Leiter
Lassen sich die Kr‰fte auch bei bewegten Ladungen in Stromleitungen beobachten?
EXP.: Wir lassen durch ein leichtbiegbares Metallband aus einem Kupferdrahtgeflecht einen Strom flieþen und f¸hren diese stromdurchflossene Leitung in ein Magnetfeld.
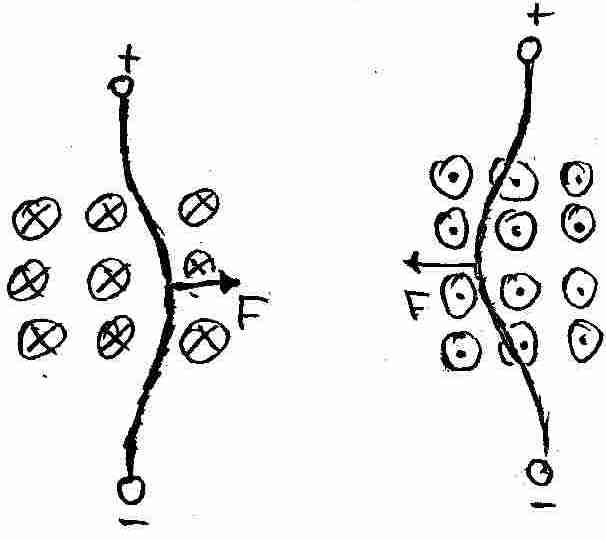
Beobachtung und Ergebnis: Man beobachtet,wie sich der Leiter senkrecht zum Magnetfeld und senkrecht zu der Bewegungsrichtung der Elektronen auslenkt. Offenbar erfahren die flieþenden Elektronen im Leiter die Lorentzkraft und ¸bertragen diese Kraft auf den Leiter.
Mithilfe von Magnetfeldern lassen sich also auf einfache Weise durch elektrische Strˆme mechanische Kr‰fte verursachen. Man nutzt dies bei Elektromotoren, die auf diesem Prinzip basieren.
-> Eigenbau eines Lorentz-Motors
70. Die magnetische Flussdichte - ein Maþ f¸r die St‰rke magnetischer Felder
Wovon h‰ngt die Grˆþe der Kraft F auf einem stromdurchflossenen Leiter im Magnetfeld ab?
Sicher von der Stromst‰rke und der Leiterl‰nge im magnetichen Feld. Aber sicher auch von der "St‰rke" des Magnetfeldes, die sich daher mithilfe dieser Kraft definieren l‰sst.
Exp.: Ein rechteckiger, stromdurchflossener Drahtrahmen befindet sich im Magnetfeld (Abb.). Da sich die Kr‰fte F1 und F2 ausgleichen, kann nur F gemessen werden.
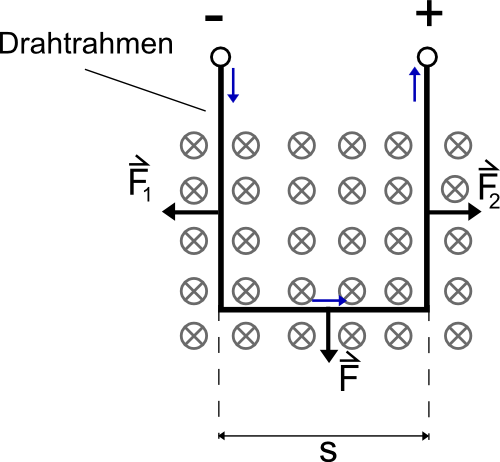
{+ErgebnisDie Kraft ist proportional zum Strom I und zur Drahtl‰nge s:
Das heiþt,
ist so lange konstant, wie wir die St‰rke des magnetischen Feldes konstant halten. Damit definieren wir als Maþ f¸r die St‰rke des Magnetfeldes die Grˆþe B: Einheit: 1 Tesla = =B wird die magnetische Flussdichte genannt. Sie l‰sst sich mit sogennanten Hallsonden leicht messen.
72. Bestimmung der Masse von Elektronen
Bestimmung der Masse durch ein Fadenstrahlrohr. Bisher haben wir in diesem Skript die Kenntnis von der Masse und der Ladung der Elektronen vorrausgesetzt. In diesem Abschnitt wird gezeigt, wie diese Masse bestimmt wird. Im n‰chsten Abschnitt geht es um die Ladung.
72.1Aufbau des Fadenstrahlrohrs
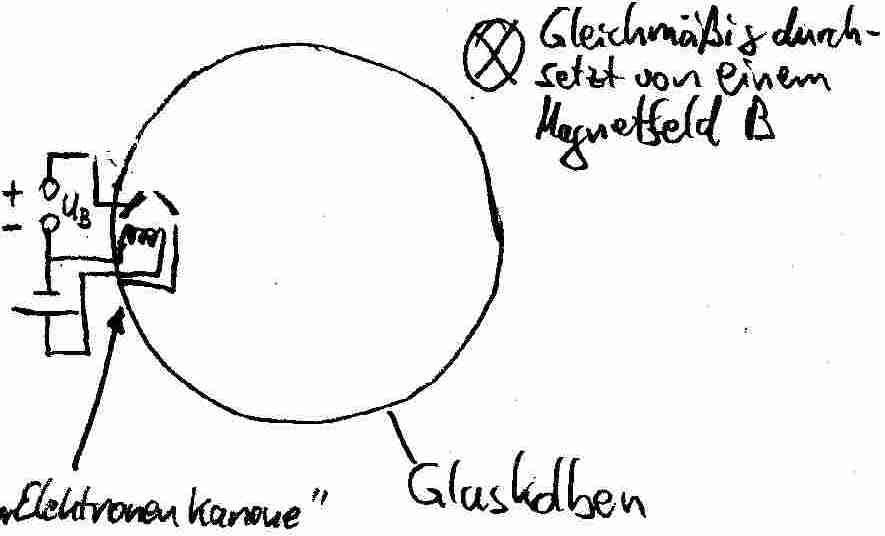
Das Fadenstrahlrohr besteht aus einem kugelfˆrmigen Glaskolben, in dessem Inneren eine Elektronenrˆhre (=Elektronenkanone) befestigt ist. Der Kolben wird von einem homogenen Magnetfeld durchsetzt, welches durch ein so genanntes Helmholtz-Spulenpaar erzeugt wird.
72.2 Geltende Zusammenh‰nge
Schaltet man die Elektronenrˆhre an, so sieht man durch eines der floreszierenden Gase der Elektronenrˆhre, dass die Elektronen auf einer Kreisbahn fliegen, desssen Radius r an einer Skala abgelesen werden kann.
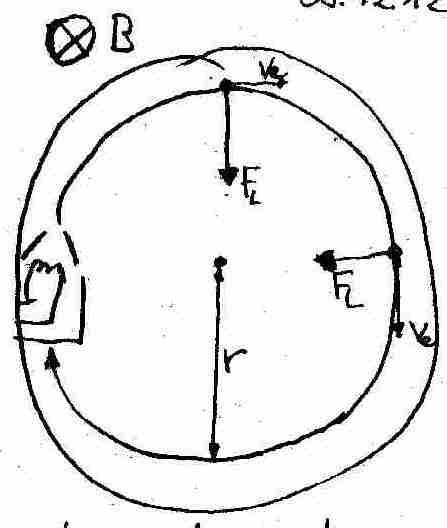
Doch wie kommt diese Kreisbahn zustande?
=> Durch die Beschleunigungsspannung UB werden die Elektronen mit der Energie
beschleunigt, wodurch diese Energie in kinetische Energie umgewandelt wird.=> Im Magnetfeld wirkt die Lorentzkraft stehts senkrecht zum Feld und zur Bewegungsrichtung des Elektrons:
=> FL zwingt die Elektronen auf eine Kreisbahn. Sie entspricht also der 'Zentripetalkraft' einer Kreisbewegung:
72.3 Bestimmung der Masse me eines Elektrons
Im n‰chsten Abschnitt wird die Elektronenladung e bestimmt. Sie betr‰gt:
Messbare Grˆþen bei diesem Experiment sind: r, UB und BNun entspricht die Zentripetalkraft der Lorentzkraft, woraus folgt: entspricht kann man k¸rzen zu:
Um me zu bestimmen, setzen wir hier
ein und quadrieren: wird zu: woraus f¸r me folgt:Setzen wir die gemessenen Grˆþen ein, erhalten wir die Elektronenmasse. Literaturwert:
74. Der Massenspektrograph
Mit einem Massenspektrograph werden die Massen von Molek¸len und Atomen, beispielsweise zur Analyse von Lebensmitteln, bestimmt. Er besteht aus einem Wien'schen Geschwindigkeitsfilter, welcher nur Teilchen einer Geschwindigkeit hindurch l‰sst, einem magnetischen Ablenkfeld und einer Fotoplatte.
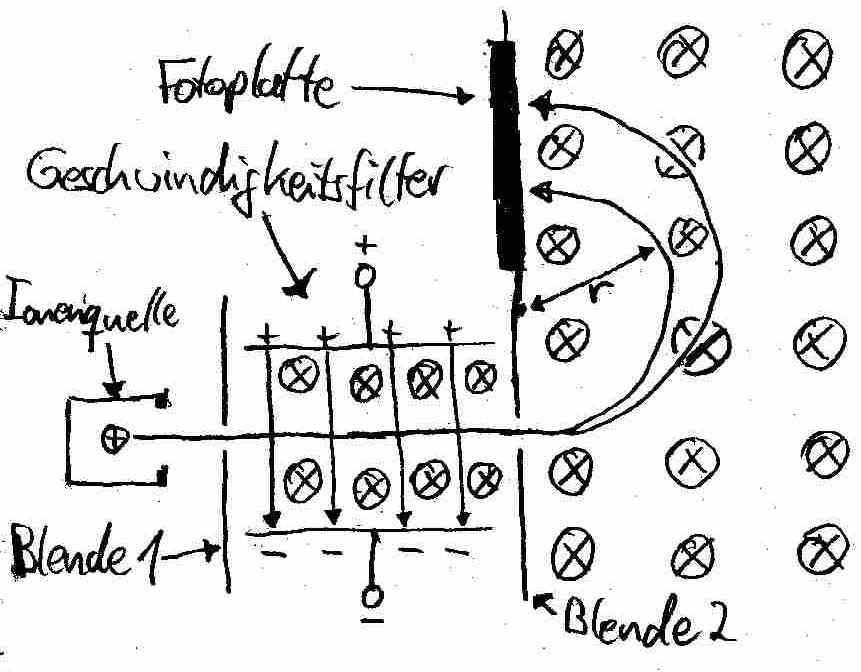
74.1 Prinzip des magnetischen Ablenkfeldes
Durch Blende 2 gelangen die Ionen mit gleicher Geschwindigkeit v in das magnetische Ablenkfeld. Hier entspricht die Lorentzkraft der Zentripetalkraft der Kreisbewegung der Teilchen mit Radius r:
-->Lˆst man nach m auf, erh‰lt man f¸r die Masse der Teilchen:
Die St‰rke des B-Feldes l‰sst sich mit Hall-Sonden messen, der Radius r kann man ¸ber die Einschlagstelle auf der Fotoplatte bestimmen, die Geschwindigkeit v kann ¸ber den Geschwindigkeitsfilter eingestellt werden und q kann als Vielfaches der Elementarladung durch logische Schl¸sse ermittelt werden. Damit sind alle Grˆþen zur Brechnung von m bekannt.
74.2 Der Wien'sche Geschwindigkeitsfilter
Der Geschwindigkeitsfilter besteht aus einem senkrecht gekreuzten, magnetischen und elektrischen Feld. Auf die positiv geladenen Ionen wirken beim Durchfliegen des Filters zwei Kr‰fte: Eine geschwindigkeitsunabh‰ngige Kraft durch das elektrische Feld E, in der Abbildung nach unten:
Und eine geschwindigkeitsabh‰ngige Kraft durch das magnetische Feld B, in der Abbildung nach oben:
Den Geschwindigkeitsfilter kˆnnen aufgrund der Blenden nur jene Teilchen passieren, die geradeaus fliegen. Das ist aber nur der Fall, wenn sich die nach oben wirkende Kraft F_L und die nach unten wirkende Kraft F_E gerade aufheben:
-->F¸r v folgt:
Nur Teilchen mit dieser Geschwindigkeit werden durchgelassen. Bleibt B konstant, kann man ¸ber
--> bestimmte Geschwindigkeiten durch anlegen der passenden Spannung U ausw‰hlen.75.: Der Halleffekt
75.1 Der Hall-Effekt kann dazu genutzt werden, auf einfache Weise die magnetische Flussdichte an Magnetfeldern zu messen. Er l‰sst sich anhand des dargestellten Bl‰ttchens erkl‰ren:
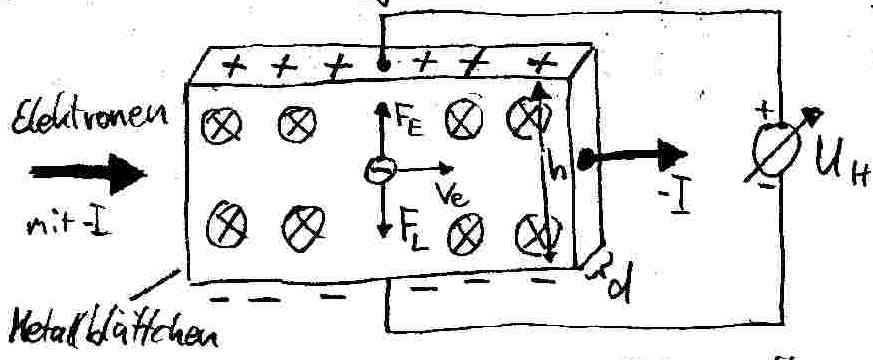
Es wird, wie gezeigt, von Elektronen durchflossen. Senkrecht zum Elektronenfluss wird es von einem Magnetfeld durchsetzt. Bewegen sich die Elektronen mit der Geschwindigkeit
, so erfahren sie die nach unten gerichtete Lorentzkraft . Dadurch sammeln sie sich an der unteren Seite des Bl‰ttchens. Dort gibt es einen Elektronen¸berschuss, w‰hrend an der Oberseite ein Elektronenmangel entsteht. Die so entstandene Spannung l‰sst sich messen. Fasst man obere und untere Bl‰ttchen als Kondensatorplatten auf, kann man daraus die Feldst‰rke berechnen. Diese bewirkt aber eine nach oben gerichtete elektrische Kraft auf die Elektronen. Wenn ghjkl so groþ geworden ist, dass sie fdjkgn ausgleicht, stiegt die Spannung nicht weiter an. Sie hat ihren Maximalwert erreicht. Es gilt dann: ==>woraus sich die folgende Hall-Spannung ergibt:
Bei einer Hall-Sonde nimmt man ein Metall mit bekannter Driftgeschwindigkeit
und errechnet mithilfe der gemessenen Hallspannung die magnetische Flussdichte:Bei bekanntem B-Feld l‰sst sich umgekehrt die Driftgeschwindigkeit der Elektronen
berechnen.75.2 Die Hall-Spannung in Abh‰ngigkeit zur Dichte der Leitungselektronen
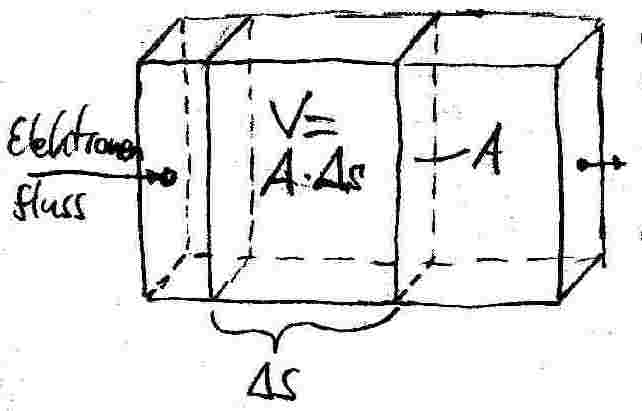
Wir betrachten nun das eingezeichnetet Volumen V des Leiterbl‰ttchens. N sei die Anzahl der Leitungselektronen in diesem Volumen. Der Strom I l‰sst sich dann wie folgt ausdr¸cken:
,da
die Driftgeschwindigkeit der Elektonen ist. Die Anzahldichte der Leitungselektronen ist nun als Anzahl pro Volumen definiert: ==>Diesen Ausdruck f¸r N kˆnnen wir in die obige Formel f¸r die Stromst‰rke einsetzen.
==>Setzen wir die Formel f¸r die Driftgeschwindigkeit in die Hallspannung ein, erhalten wir:
Dies ist die Formel der Hallspannung in Abh‰ngigkeit zur Dichte der Leitungselektronen. Mit ihr l‰sst sich besagt Dichte durch Umstellen bestimmen:
76.: Das Magnetfeld einer lang gestreckten Spule
Die St‰rke des Magnetfeldes im Innern einer lang-gestreckten Spule h‰ngt vermutlich ab von:
- der Stromst‰rke I
- der Windungsdichte (Anzahl Windungen pro Meter)
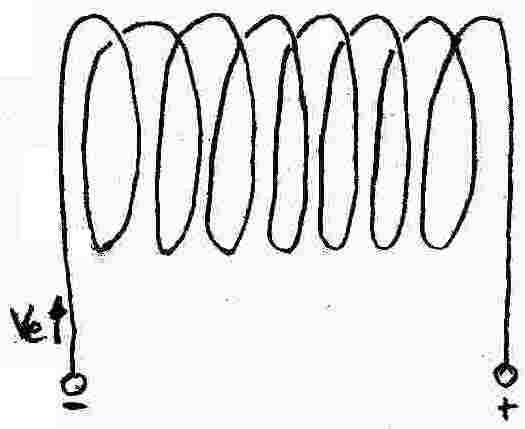
Diese Vermutungen lassen sich experimentell durch Spulen verschiedener Bauart best‰tigen. Es l‰sst sich auch experimentell darstellen, dass B im Innern der Spule nicht vom Spulendurchmesser oder von der L‰nge l der Spule abh‰ngt, wenn obige Grˆþen konstant bleiben.
Vermutung ¸ber den quantitativen Zusammenhang:
mit der Proportionalit‰tskonstanten==> Exp.: Die Formel wird durch Messungen an verschiedenen Spulen best‰tigt. Die Proportionalist‰tskonstante
kann aus den Messwerten bestimmt werden:Man nennt sie magnetische Feldkonstante.
==> Exp.: Steckt man in die Spule einen ferromagnetischen Stoff, so verst‰rkt sich die Flussdichte um einen Faktor
. ist eine Materialkonstante und wird Permeabilit‰tszahl gennant. Allgemein gilt bei lang gestreckten Spulen:77. Induktion in einem geraden Leiterst¸ck
Magnetische Felder ¸ben auf stromdurchflossene Leiter Kr‰fte aus, soviel ist bereits bekannt: Legt man, wie dargestellt, auf zwei ebene, runde Metallstangen im Magnetfeld eine dritte, frei bewegliche und l‰sst durch diesen den Strom I flieþen, so wirkt die Lorentzkraft auf die Elektronen und die bewegliche Stange wird mit der Kraft F = B*I*d beschleunigt. Anwendungsgebiete sind Elektromotoren, die elektrische Energie in mechanische Energie wandeln. Doch: Kann man auch umgekehrt mechanische in elektrische Energie wandeln? => Kehren wir das obige Experiment einfach um !
Wie seitlich dargestellt lassen wir jetzt eine Stativstange durch das Magnetfeld rollen und stellen fest: es entsteht tats‰chlich eine Spannung Uind, die wir Induktionsspannung nennen.
Wie kˆnnen wir ihr Zustandekommen erkl‰ren? Zusammen mit der Stange bewegen sich auch die in ihr enthaltenen Leitungselektronen mit der Geschwindigkeit vs senkrecht zu den Magnetfeldlinien. Dadurch wirkt auf sie aber die Lorentzkraft FL, weshalb sie sich nach unten bewegen. In der Folge l‰dt sich die untere Stange negativ und die obere positiv auf. Hierdurch entsteht jedoch ein elektrisches Feld E, welches eine zur Lorentzkraft entgegen gesetzte elektrische Kraft auf das Elektron aus¸bt. Die maximale Spannung Uind zwischen den Stangen wird erreicht, wenn die Kr‰fte im Gleichgewicht sind: (negatives Vorzeichen, da die Kraftrichtung entgegen gesetzt ist)
mit folgt=>
So l‰sst sich die Induktionsspannung aus B, d und vs berechnen.
78. Magnetischer Fluss und Flussdichte und deren anschauliche Bedeutung
Magnetische Flussdichte:
Wir haben die magnetische Flussdichte B als Maþ f¸r die St‰rke des magnetischen Feldes kennen gelernt. Stellen wir uns Magnetfelder durch Feldlinien repr‰sentiert vor, so sind sie dort besonders stark, wo die Feldlinien besonders dicht sitzen. Der Begriff der Flussdichte entstammt nun genau dieser Vorstellung: Denkt man sich eine Ebene, die senkrecht von einem homogenen Magnetfeld durchdrungen wird, so kann man sich die Flussdichte anschaulich als die Dichte der die Ebene durchdringenden Feldlinien ("Feldlinien pro Fl‰che") vorstellen. Diese Vorstellung geht auf Michael Faraday (1791-1867) zur¸ck.
Magnetischer Fluss:
Der magnetische Fluss hatte f¸r Faraday die Bedeutung der Anzahl an Feldlinien, die eine bestimmte Fl‰che senkrecht durchdringen. Der magnetische Fluss h‰ngt damit nicht nur von der St‰rke des Feldes (Der Flussdichte) ab, sondern auch von der Grˆþe der Fl‰che: Je grˆþer die Fl‰che, desto mehr Feldlinien durchdringen sie und desto grˆþer ist somit der magnetische Fluss.
W‰hrend die Flussdichte mit B abgek¸rzt wird, erh‰lt der magnetische Fluss das Symbol Φ (groþes griechisches "Phi"). Weil die Flussdichte als Feldlinien pro Fl‰che gedacht werden kann, erh‰lt man die Anzahl der Feldlinien durch eine Fl‰che A durch die Multiplikation der Flussdichte mit der Fl‰che:
Einheit:
81. Induktionsspannung in Spulen
Bei einer Spule mit n-Windungen handelt es sich im Grunde um n hintereinandergeschaltete Leiterschleifen. F¸hrt man eine solche Spule entsprechend in ein Magnetfeld ein, so addieren sich die Induktionsspannungen der einzelnen Windungen. FÐr eine Spule mit n Windungen gilt somit:
82.: Induktion auch ohne Bewegung?
Die Formel
sagt aus, dass die Induktionsspannung in einer Leiterschleife von der Windungsanzahl und der ƒnderungsrate (= Ableitung)des magnetischen Flusses abh‰ngt. Der magnetische Fluss ‰nder sich, wenn sich die von dem Magnetfeld durchdrungene Fl‰che A der Leiterschleife ‰ndert. F¸r eine konstante Flussdichte B folgt also wegen (bei konstanten B), wenn die Fl‰chen‰nderung pro Zeit ist.Der magnetische Fluss ‰ndert sich aber auch, wenn sich die Flussdichte B ‰ndert, w‰hrend die Fl‰che A konstant bleibt - also dann, wenn wir die Spule nicht bewegen, sondern lediglich die St‰rke des Magnetfeldes ‰ndern. Doch: Wird dann auch eine Spannung induziert? Gilt also:
(bei konstanter Fl‰che) ?Pr¸fen wir diese Formel an einem Experiment!
Exp.: ==> Das sich ‰ndernde Magnetfeld erzeugen wir durch eine lang gestreckte Spule, die innen hohl ist, indem wir den durch sie flieþenden Strom ‰ndern.
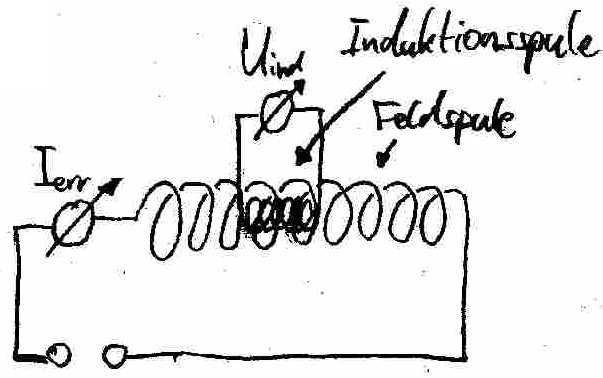
Wegen
betr‰gt die ƒnderungsrate des Magnetfeldes , wenn der Strom mit der Rate vergrˆþert oder verkleinert wird. Um zu messen, lassen wir den Strom linear ansteigen. entspricht dann der Steigung im I-t-Diagramm. ==> Anschlieþend messen wir die Spannung an einer Spule, die in den Hohlraum der groþen Erregerspule hineingeschoben wird und vergleichen die gemessene Spannung mit der errechneten:==> Ergebnis: Der gemessene Wert f¸r die Induktionsspannung stimmt mit dem berechneten Wert bestens ¸berein.
Schlussfolgerung: Auch durch die reine ƒnderung der Flussdichte wird eine Spannung - wie durch das Faraday'sche Induktionsgesetze vorhergesagt - in die ansonsten ruhende Leiterschleife induziert. Dies l‰sst sich nicht durch Lorentzkr‰fte erkl‰ren.
mit ist somit ein allgemeines Gesetz, aus dem die beiden Spezialf‰lle folgen: ==> (bei konstantem B-Feld) ==> (bei konstanter Fl‰che A)83. Elektrische Wirbelfelder
Verbinden wir den "+"-Pol einer Spannungsquelle U ¸ber einen Kupferdraht mit dessen "-"-Pol, so flieþt deshalb ein Strom, wie ¸ber die L‰nge d des Drahtes die elektrische Feldst‰rke
die Elektronen mit der Kraft von "-" nach "+" treibt.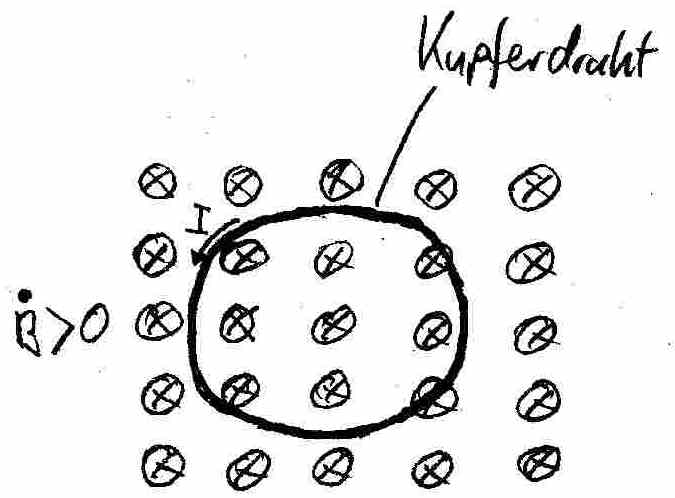

Gehen wir aber, wie oben dargestellt, von einem zu einem Ring geschlossenen, sich nicht bewegenden Kupferdraht aus, welcher sich in einem st‰rker werdenden Magnetfeld befindet, so kˆnnen wir experimentell einen Kreisstrom feststellen, welcher aufgrund der Induktionsspannung U_ind flieþt. Da sich der Kupferring nicht bewegt, kˆnnen wir es nicht ¸ber die Lorentzkraft erkl‰ren, dass sich die Elektronen im Draht in Bewegung setzen. Wir m¸ssen also annehmen, dass das sich ver‰ndernde Magnetfeld ein ringfˆrmiges elektrisches Feld erzeugt, welches die Elektronen durch den Draht zieht. Da dieses Feld weder Anfang noch Ende hat, nennen wir es elektrisches Wirbelfeld. Seine Existenz kˆnnen wir durch die sogenannte elektrodenlose Ringentladung pr¸fen.
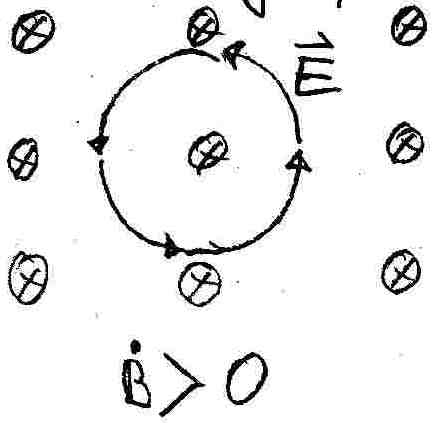
85. Anwendungen elektrischer Wirbelfelder
Elektrische Wirbelfelder haben zahlreiche Anwendungen. Zwei Beispiele:
=>Induktionsherde Durch sich stark ‰ndernde Magnetfelder wird im Boden der Kochtopfer ein starker Wirbelstrom induziert. Elektrische Energie wird wegen des Stroms dort in W‰rme umgewandelt, wo sie gebraucht wird: Im Topf!
=>Transformatoren Eine Prim‰rspule erzeugt ein zeitlich schankendes Magnetfeld. Durch das elektrische Wirbelfeld wird in einer Sekujnd‰rpule eine Spannung induziert, dessen Grˆþe von der Anzahl der Windungen abh‰ngt.
87. Der Zusammenhang zwischen Lenz'schem Gesetz & Energieerhalungssatz
Bei dem rechts gezeichneten Experiment handelt es sich um den selben Aufbau wie in Nr. 77:
Eine Metallstange rollt durch ein Magnetfeld, wodurch die Spannung U_ind= -B*d*v_s induziert wird. Durch die Spannung flieþt der Strom I durch die Lampe, welche mit der Leistung P= U*I leuchtet. Nach der Zeit t wurde also folgende elektrische Arbeit verrichtet:
Aber wo kommt diese Energie her? Wird sie tats‰chlich aus dem Nichts erzeugt? Der Strom flieþt auch durch die vollende Metallstange. Damit erf‰hrt sie die eingezeichnete Kraft
entgegen der Bewegungsrichtung. Die mechanische Arbeit, die verrichtet werden muss, um die Geschwindigkeit v_s aufrecht zu erhalten, l‰sst sich ¸ber die Definitionsgleichung der Arbeit berechnen:Hieraus l‰sst sich sehen, dass die aufgrund der Induktion verrichtete elektrische Arbeit der Arbeit entspricht, die am Stab mechanisch verrichtet werden muss, um die Bewegung aufrecht zu erhalten. Es handelt sich also nur um einen Umwandlungsprozess von mechanischer Energie in elektrische Energie.
Hiermit begr¸ndet sich auch die Lenz'sche Regel:
Der induzierte Strom verursacht eine Kraft, die seiner Ursache (der Bewegung des Stabs durch das magnetische Feld) entgegen wirkt.
90. Die Induktivit‰t (oder auch Eigeninduktivit‰t)
Kˆnnen wir die "Eigeninduktionsspannung" auch berechnen?
Nun: I' gibt an, um wie viel Ampere der Strom pro Sekunde ansteigt. Weil Mu0, Mur, N und l konstant sind, steigt B mit der Rate
an, woraus folgt (Wenn die Spulenfl‰che A konstant bleibt):
Da es sich bei der Feldspule auch um die Induktionsspule handelt, ist n = N, woraus f¸r die Induktionsspannung nun folgt:
Der Vorfaktor von I' besteht also nur aus konstanten Spuleneigenschaften. In der Physik nennt man den, von den Spuleneigenschaften abh‰ngigen Faktor
auch die Induktivit‰t (auch: Eigeninduktivit‰t) der Spule. Je grˆþer die Induktivit‰t einer Spule ist, desto grˆþer ist die in ihr induzierte Spannung bei gleichbleibender ƒnderungsrate des durch ihr flieþenden Stromes:
Einheit von L:
91. Selbstinduktion - Der Einschaltvorgang

Die Gesamtspannung U'(t) an der Spule setzt sich beim Einschaltvorgang aus der von auþen angelegten Spannung U0 und der Induktionsspannung zum Zeitpunkt t
zusammen:Die Spule hat den Widerstand R, ¸ber den sich mit U(t) der durch sie und den Stromkreis flieþenden Strom I(t) berechnen l‰sst:
Hieraus erhalten wir die Differentialgleichung f¸r den Einschaltvorgang.
Hat sich das Mu-Feld fertig aufgebaut und ist daher Utext(ind) = 0, so flieþt der maximale Strom
. Mit dieser Bezeichnung erhalten wir f¸r unsere DGL die entg¸ltige Form:Wir suchen jetzt eine Funktion f¸r den Strom, welche die DGL erf¸llt.
Experiment: Um einen Ansatz f¸r die Stromfunktion I(t) zu erhalten, zeichnen wir mit CASSY den Messwertgraphen aus obiger Schaltung:
Ergebnis: Ansatz:
/-I_max und vorklammern
/ :(Imax * e^(-R/L *)
/+1 / * R/L
1 = 1
- Die DGL wird durch folgende Funktion gelˆst:
Die Funktion gibt die Stromst‰rke zum Zeitpunkt t nach dem Einschalten wieder.
99. Ideenfindundung: Wie kann man Schwingungen mathematisch beschreiben?
Um Schwingungen mathematisch erfass- und berechenbar zu machen, m¸ssen wir wissen, mit welcher Funktion wir die Auslenkung y(t) des schwingenden Kˆrpers beschreiben kˆnnen.
Experiment: Wir erfassen die Schwingungen der Kugel ¸ber einen Faden mit dem CASSY und stellen die Auslenkung graphisch als Funktion der Zeit dar.
Ergebnis: Der Graph sieht sinusfˆrmig aus. Vermutlich l‰sst sich also die zeitliche Auslenkung y(t) ¸ber eine Sinusfunktion beschreiben. Um diesen Ansatz pr¸fen zu kˆnnen, m¸ssen wir uns im n‰chsten Abschnitt zun‰chst noch einmal anschauen, wie der Sinus mathematisch definiert ist.
105.Definition der haromonischen Schwingung
Eine Schwingung, die mit dem Ansatz
beschrieben werden kann, nennt man harmonische Schwinugung. Generell sind alle Schwingungen harmonisch, deren R¸ckstellkraft proportional zur Auslenkung ist, wie beim Spiralfederpendel:
Solche Schwingungen lassen sich durch Differentialgleichungen der Form
beschreiben.