Die Selbstinduktion
In der unten abgebildeten Schaltung ist die Lampe L1 und eine Spule mit Eisenkern zu einer baugleichen Lampe L2 und einem Widerstand R parallel geschaltet. Der Widerstand R ist genau so groß gewählt, wie der Widerstand der Spule.
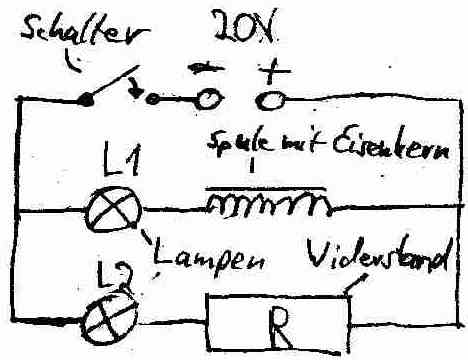
Experiment: Über den Schalter wird der Stromkreis geschlossen. Wir beobachten, dass L2 sofort mit dem Umlegen des Schalters leuchtet. L1 leuchtet jedoch erst mit Verzögerung: Innerhalb einer Sekunde steigt ihre Helligkeit auf das Niveau von L1.
Doch wie kommt diese zeitliche Verzögerung zustande?
Erklärung: Kurz nach dem Umlegen des Schalters fließt durch die Spule jetzt mehr und mehr Strom. Mit dem Strom baut sich auch das Magnetfeld der Spule
immer mehr auf, wodurch auch der magnetische Fluss Φ = AB durch die Spule ansteigt:
Offenbar wird nun, durch den steigenden Fluss, in der Spule selbst eine Spannung induziert, welche der Spannung des Netzgerätes entgegen gerichtet ist. Das verzögert das Ansteigen des Stromes durch die Spule und durch die Lampe L1. Erst, wenn der maximale Strom durch die Spule I_Max erreicht ist, ändert sich der magnetische Fluss durch die Spule nicht mehr, und der Strom kann ungehindert durch sie hindurch fließen. Erst jetzt leuchtet sie also gleich hell wie die Lampe L2.Zusammengefasst:
- Wir der Strom durch eine Spule eingeschalten, so baut sich das Spulenfeld auf und der magnetische Fluss durch die Spule erhöht sich. Dadurch wird in die Spule selbst eine Spannung induziert. Diesen Vorgang nennt man Selbstinduktion.
- Die Induktionsspannung ist gemäß der Lenz'schen Regel so gerichtet, dass er das Ansteigen des Spulenstroms (und damit seiner Ursache) entgegen wirkt.
Die Induktivität (oder auch Eigeninduktivität)
Können wir die "Eigeninduktionsspannung" auch berechnen?
Nun: Die Ableitung des Stroms I' gibt an, um wie viel Ampere der Strom pro Sekunde ansteigt. Weil my0, myr, N und l konstant sind, steigt B mit der Rate
an. Bei konstant bleibender Spulenfläche wächst der magnetische Fluss Phi durch die Spule proportional zur magnetischen Flussdichte B an:
Da es sich bei der Feldspule auch um die Induktionsspule handelt, ist n = N, woraus für die Induktionsspannung nun folgt:
Im Prinzip haben wir unser Ziel, die Eigeninduktionsspannung zu berechnen, erreicht. Allerdings ist der Formelausdruck recht kompliziert. Mit einer hilfreichen neuen physikalischen Größe, können wir ihn stark vereinfachen:
Der Vorfaktor von I' besteht nur aus konstanten Spuleneigenschaften. In der Physik nennt man den von den Spuleneigenschaften abhängigen Faktor
auch die Induktivität (auch: Eigeninduktivität) der Spule. Die Induktivität ist eine Spuleneigenschaft. Je größer die Induktivität einer Spule ist, desto größer ist die in ihr induzierte Spannung bei gleichbleibender Änderungsrate des durch ihr fließenden Stromes:
Die Einheit von L wird Henry genannt:
Zusammengefasst:
- Ändert sich der Strom durch eine Spule, so wird in diese Spule eine Spannung induziert, welche durch die folgende Gleichung berechnet werden kann:
- Der Faktor L ist eine Spuleneigenschaft, die mit Induktivität bezeichnet wird. Von ihr hängt ab, wie groß die Induktionsspannung bei Änderung des Spulenstroms ist.
- Die Induktivität einer lang gestreckten Spule kann man berechnen durch
Selbstinduktion - Der Einschaltvorgang
In diesem Abschnitt werden wir eine Funktion finden, die den Anstieg des Spulenstroms beim Einschaltvorgang richtig beschreibt. Ähnlich wie beim Lade/Entladevorgang von Kondensatoren, führt auch hier der Weg über eine Differentialgleichung, die wir jetzt herleiten.

Die Gesamtspannung U'(t) an der Spule setzt sich beim Einschaltvorgang aus der von außen angelegten Spannung U0 und der Induktionsspannung zum Zeitpunkt t
zusammen:Die Spule hat den Widerstand R, über den sich mit U(t) der durch sie und den Stromkreis fließenden Strom I(t) berechnen lässt:
Hieraus erhalten wir schließlich die Differentialgleichung für den Einschaltvorgang.
Hat sich das B-Feld fertig aufgebaut und ist daher Uind = 0, so fließt der maximale Strom
. Mit dieser Bezeichnung erhalten wir für unsere DGL die entgültige Form:Wir suchen jetzt eine Funktion für den Strom, welche die DGL erfüllt.
Experiment:
Um einen Ansatz für die Stromfunktion I(t) zu erhalten, zeichnen wir mit CASSY den Messwertgraphen aus obiger Schaltung. Der Graph (nicht im Skript enthalten) legt folgenden Ansatz für die Funktion nahe:
Ergebnis: Ansatz:
wobei lambda eine noch zu bestimmende Konstante ist.
Für die Ableitung folgt
Wir prüfen den Ansatz durch Einsetzen in die DGL und prüfen, unter welcher Bedingung er sie erfüllt:
... wir ziehen beidseitig I_max ab ...
... und teilen durch die gemeinsamen Faktoren...
... woraus für lambda folgt:
Die DGL wird also durch folgende Funktion gelöst:
Die Funktion gibt die Stromstärke durch die Spule zum Zeitpunkt t nach dem Einschalten wieder.
Zusammengefasst:
- Der Verlauf des Spulenstroms beim Einschaltvorgang einer Spule wird durch folgende Differentialgleichung beschrieben:
- Die DGL wird durch diese Funktion gelöst:
Selbstinduktion - Der Ausschaltvorgang

Ist der Schalter S geschlossen, so besteht in der Spule ein Magnetfeld, welches durch den Strom verursacht wird.
Wird der Schalter dann geöffnet, verursacht das Abfallen des magnetischen Flusses eine Induktionsspannung, welche ihrer Ursache (d.h. dem abfallenden Strom) entgegen wirkt. Damit wird der Stromfluss über den inneren Stromkreis aufrecht erhalten.
Der Strom zirkuliert somit im inneren Stromkreis. Aufgrund des Widerstands R der Spule, wandelt sich die elektrische Energie nach und nach in Wärme um, wodurch der von der Induktionsspannung verursachte Strom langsam abebbt.
Wir wollen nun versuchen, eine Funktion I(t) zu finden, welche den zeitlichen Verlauf des abebbenden Stroms nach Schalteröffnung richtig beschreibt. Dazu stellen wir zunächst eine DGL auf:
Die Spannung UR am Spulenwiderstand ist gleich der Induktionsspannung. Wegen U=I*R folgt:
Durch Umformungen folgt die gesuchte Differentialgleichung für den Ausschaltvorgang:
Doch welche Funktion für I(t) löst diese Differentialgleichung?
Experiment:
Um einen Ansatz zu finden, zeichnen wir experimentell die Messwertkurve für I(t) mit dem CASSY auf. Dabei stellen wir einen exponentiellen Abfall fest. Die Vermutung liegt also nahe, dass folgender Ansatz den Verlauf des Stroms richtig beschreibt:
Prüfung des Ansatzes:
Wir können den Ansatz prüfen, indem wir ihn in die DGL einsetzen und prüfen, ob er die Gleichung erfüllt.
Für die Ableitung von des Stromes I'(t) folgt aus dem obigen Ansatz:
Setzen wir die Funktion und ihre Ableitung in die DGL ein, erhalten wir
Teilt man die Gleichung durch den Faktor
, so bekommen wirHieraus folgt direkt
wodurch wir die folgende Funktion gefunden haben, die den zeitlichen Verlauf des Stroms richtig beschreibt:
Zusammengefasst:
- Der Verlauf des Spulenstroms beim Ausschaltvorgang einer Spule wird durch folgende Differentialgleichung beschrieben:
- Die DGL wird durch diese Funktion gelöst:
Die Halbwertszeit des Stromes beim Ausschaltvorgang
Über die Stromfunktion I(t) können wir jetzt leicht herausfinden, wie lange es dauert, bis der induzierte Strom auf die Hälfte seiner ursprünglichen Größe abgesunken ist:
Beidseitiges Logarithmieren ergibt schließlich
Zusammengefasst:
- Die Zeit, innerhalb der sich der Strom beim Ausschaltvorgang einer Spule halbiert, beträgt
94.Das RL-Glied
Sind Induktivität und Widerstand, wie unten dargestellt, in Reihe geschaltet, so spricht man vom RL-Glied.
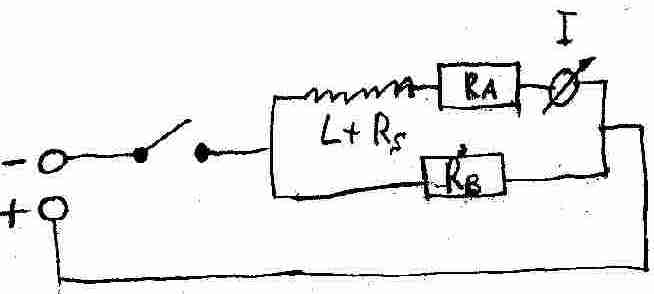
Wir können den Strom I(t) zum Zeitpunkt t mit den in den obigen Abschnitten hergeleiteten Formeln berechnen. Der Widerstand R entspricht der Summe der mit der Spule in Reihe liegenden Widerständen.
Für den Einschaltvorgang verwendet man
mit
Für den Ausschaltvorgang entsprechend
mit
Energie des magnetischen Feldes
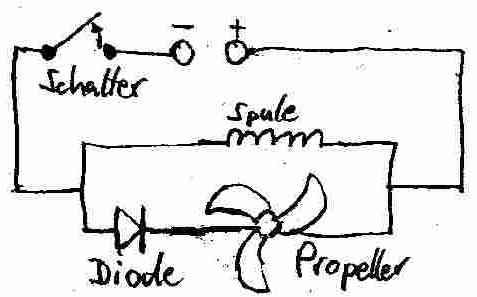
Ist in der oben dargestellten Schaltung der Schalter geschlossen, so fließt nur über die Spule ein Strom, da die Diode den Stromfluss in gleicher Richtung über den Propeller verhindert.
Öffnet man den Schalter, so baut sich das Magnetfeld in der Spule ab und verursacht einen Induktionsstrom. Die Elektronen fließen im Uhrzeigersinn durch den inneren Stromkreis - und damit in Durchlassrichtung der Diode. Wir beobachten, dass sich der Propeller dreht.
... doch: Warum dreht sich der Propeller? Schließlich kann wegen des offenen Schalters keine Energie mehr von der Stromquelle nachfließen.
Offenbar ist im magnetischen Feld Energie gespeichert. Bei Verringerung des magnetischen Flusses wandelt sich die Energie dieses Feldes dann über den Induktionsstrom in elektrische Energie um.
Wir werden jetzt versuchen, eine Formel zu finden, mit der wir ausrechnen können, wie viel Energie in dem Feld einer Spule mit Induktivität L steckt, wenn wir den Strom I durch sie hindurch fließen lassen. Dazu betrachten wir diesen Ausschaltvorgang genauer:
Die Leistung, die im ganzen inneren Stromkreis geleistet wird, lässt sich einfach berechnen:
Bezeichner R den elektrischen Widerstand des Kreises, so kann man U durch U = I * R ausdrücken.
Leistung ist definiert als Arbeit pro Zeit. Das bedeutet: Im Zeitraum Δt gilt für die über diesen Zeitraum durchschnittliche Leistung
Die momentane Leistung zu einem Zeitpunkt t ist dann
Die momentane Leistung zum Zeitpunkt t ist also die Ableitung der verrichteten Arbeit zu diesem Zeitpunkt.
Die ursprünglich im Magnetfeld gespeicherte Energie entspricht nun der über den gesamten Zeitraum verrichteten Arbeit. Da P offenbar die Ableitung der Arbeit ist, erhalten wir die über den gesamten Zeitraum verrichtete Arbeit, indem wir P(t) von t=0 bis t=∞ integrieren:
Setzt man für I die für den Ausschaltvorgang hergeleitete Formel ein, folgt:
R und I_0 sind konstant bleibende Zahlen und können daher vor das Integral geschrieben werden:
Multiplizieren wir die Klammern aus, erhalten wir die gesuchte Formel für die Magnetfeldenergie:
Fließt also durch eine Spule mit der Induktivität L der Strom I, so enthält das Magnetfeld der Spule die Energie
Zusammengefasst:
- Ähnlich wie bei den elektrischen Feldern, so speichern auch magnetische Felder Energie.
- In dem Magnetfeld einer mit dem Strom I durchflossenen Spule, welche die Induktivität L besitzt, ist folgende Energie gespeichert:
Die Energiedichte des magnetischen Feldes
Doch sitzt die Energie wirklich im magnetischen Feld? - Wenn ja, müsste die Energie W_mag proportional zum vom Feld durchsetzen Volumen sein.
Betrachten wir das Feld
einer lang gestreckten Spule. Für ihre Induktivität haben wir bereits die Formel
hergeleitet und können Sie direkt in die Formel für die Energie des Magnetfeldes einsetzen:
Wir formulieren die rechte Seite der Gleichung etwas um:
Durch Kürzen kann man sehen, dass hier nichts anderes steht, als auf der rechten Seite der darüber liegenden Gleichung. Nur wird in dieser Schreibweise einiges sichtbar: Die hinteren Faktoren entsprechen nämlich der magnetischen Flussdichte zum Quadrat:
Multipliziert man die Grundfläche A der Spule mit dessen Länge l, so erhält man ihr Volumen. Der folgende, ebenfalls in obiger Gleichung steckende Faktor entspricht also dem Volumen des vom Magnetfeld durchdrängten Spuleninneren:
Mit diesen Kenntnissen erhalten wir die Formel
Tatsache: Wmag ist proportional zu V. Die Energie sitzt tatsächlich in dem Feld, welches das Volumen V durchdringt.
Da die Energie im Feld gespeichert wird, macht es Sinn, eine Energiedichte zu definieren, welche angibt, wie viel Energie das Feld pro Volumeneinheit enthält.