SDL-SERVER PhysikSkript/Magnete und Magnetfelder
PhysikSkript

Magnete und Magnetfelder

  1. Magnete und magnetische Kräfte
  2. Ferromagnetische Stoffe
  3. Separation der Pole eines Magneten
  4. Modell der Elementarmagnete
  5. Das magnetische Feld
  6. Magnetfelder durch Ströme
  7. Das Magnetfeld einer stromdurchflossenen Spule
  8. Die Lorentzkraft
  9. Kraft auf stromdurchflossene Leiter
  10. Die magnetische Flussdichte - ein Maß für die Stärke magnetischer Felder
  11. Die Lorentzkraft berechnen
  12. Das Magnetfeld einer lang gestreckten Spule
  13. Bestimmung der Masse von Elektronen
  14. Der Massenspektrograph
  15. Der Halleffekt

Magnete und magnetische Kräfte

Experiment:
Ein starker, scheibenförmiger Magnet wird auf eine glatte Tischoberfläche gelegt. Dabei beobachtet man, dass egal wie rum man ihn auf den Tisch dreht, sich immer wieder die selbe Seite in Richtung Norden und die entgegengesetze Seite in Richtung Süden ausrichtet.

Schlussfolgerung und Definition:
Ein Magnet hat zwei Pole. Die Seite des Magneten, die sich immer in Richtung Norden dreht, nennen wir Nordpol des Magneten, die entgegengesetze Seite Südpol des Magneten. Der Nordpol ist meist mit rot, der Südpol meist mit grün markiert.

Experiment:
Wir halten die verschiedenen Pole eines Magneten aneinander.

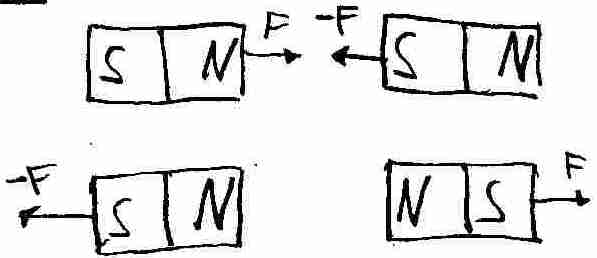
Ergebnis:
Analog zu den Ladungen ziehen sich ungleichnamige Pole an, gleichnamige Pole stoßen sich ab.

Zusammengefasst:

  • Von Magneten gehen anziehende und abstoßende Kräfte aus.
  • Magnete bestehen aus zwei Polen: Sie werden Nordpol und Südpol genannt.
  • Ungleichnamige Pole ziehen sich an, gleichnamige stoßen sich ab.

Ferromagnetische Stoffe

Neben den Kräften zwischen Magneten, ziehen Magneten auch bestimmte andere Stoffe an. Diese sind Eisen(Fe), Kobalt(Co) und Nickel(Ni). Man nennt diese Stoffe deshalb ferromagnetische Stoffe. Andere Stoffe werden von Magneten nicht angezogen.

"Ferro" kommt von der lateinischen Bezeichnung "Ferrum" für Eisen. Ferromagnetische Stoffe haben also gleiche/ähnliche Eigenschaften wie Eisen. Nickel und Kobalt sind ebenso magnetisierbar - genau wie Eisen.

Diese Stoffe lassen sich demnach auch magnetisieren, indem man sie immer in die selbe Richtung an einem Magneten vorbei reibt. Dies wird in der folgenden Abbildung am Beispiel einer Eisennadel dargestellt:

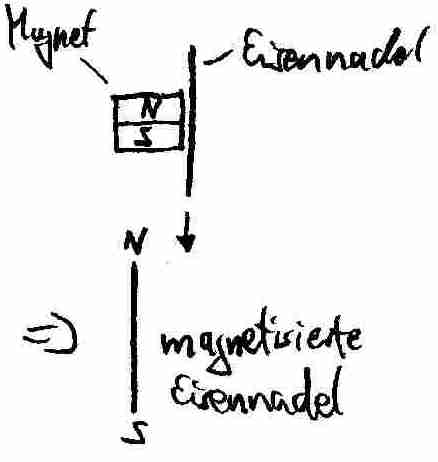
Allgemein gilt: Körper, die von Magneten angezogen werden, sind auch selbst magnetisierbar.

Zusammengefasst:

  • Nicht auf alle Stoffe, sondern nur auf ferromagnetische Stoffe lassen sich magnetische Kräfte direkt beobachten.
  • Ferromagnetische Stoffe sind selbst auch magnetisierbar.

Separation der Pole eines Magneten

Exp.: Wir versuchen jetzt den Nordpol eines Magneten von seinem Südpol zu trennen. Dazu nehmen wir eine magnetisierte Eisennadel aus 62. und teilen sie mit einer Zange in zwei Teile.

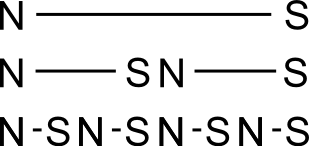
Ergebnis: Beide Teile haben nach wie vor Nord- und Südpol. Der Vorgang lässt sich beliebig oft wiederholen.

Wie lassen sich diese Effekte erklären? -> Modell Elementarmagnete

Zusammengefasst:

  • Es gibt keine magnetischen Monopole. Ein Magnet hat immer beides: Nord- UND Südpol.

64. Modell der Elementarmagnete

Man stellt sich vor, dass ferromagnetische Stoffe aus vielen, sehr kleinen und nicht weiter teilbaren Magneten, den sogenannten Elementarmagneten, besteht. Mit dieser Vorstellung lassen sich alle Effekte der Magnetostatik erklären:

In nichtmagnetisierten Stoffen sind die Elementarmagnete ungeordnet und heben sich in ihrer magneteischen Wirkung auf. Der ferromagnetische Körper als Ganzes bildet damit keine Pole aus.
Streicht man den ferromagnetischen Stoff entlang einem Magneten, so richten sich die Elementarmagnete an den Polehn des Magneten aus und richten sich zum größten Teil aus.Dadurch verstärken die Elementarmagnete ihre Wirkung und der ferromagnetische Stoff bildet selbst Pole aus.
In der Abbildung richten sich die Elementarmagnete nach dem von links angenäherten Südpol aus. Dadurch wird der ferromagnetische Stoff selbst zum Magneten.

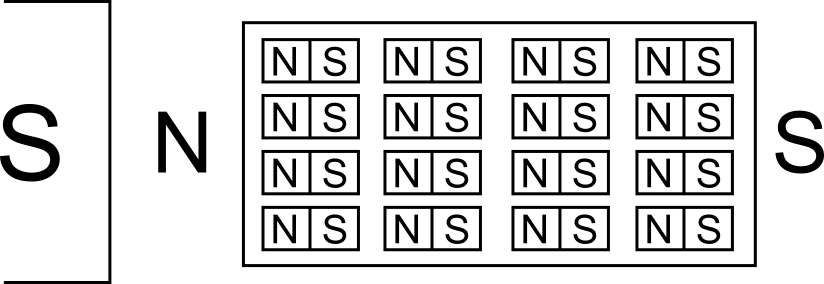
Teilt man den magnetisierten Stoff, bleibt die Ausrichtung der Elementarmagnete bestehen. Beide Pole sind, wie in der unteren Abbildung dargestellt, in beiden Bruchstücken vorhanden.

Durch Erhitzung oder starke mechanische Schläge kann die Ordnung der Elementarmagnete wieder zerstört werden. Der ferromagnetische Stoff hat dann seine Magnetisierung verloren. Er ist entmagnetisiert.
Lässt sich ein Körper leicht magnetisieren und wieder entmagnetisieren, bzw. lassen seine Elementarmagneten leicht ausrichten, so bezeichnet man diesen Stoff als magnetisch weich.

Wichtig ist: Wegen der Unteilbarkeit der Elementarmagnete gibt es keine magnetischen Monopole. Hierdurch unterscheiden sich Magnete von geladenen Körpern: Magnete haben immer zugleich einen Nord- wie einen Südpol.

Zusammengefasst:

  • Das Modell der Elementarmagnete besagt, dass Magnete aus sehr vielen kleinen Elementarmagneten bestehen, die sich nicht weiter teilen lassen.
  • Alle bisher beobachteten Effekte lassen sich auf der Grundlage dieses Modells erklären.

Das magnetische Feld

Ähnlich wei beim elektrischen Feld geht man davon aus, dass die Kräfte zwischen Magneten durch magnetische Felder vermittelt werden.
Vorstellen kann man sich das so: Wenn man einen Nagel in die Nähe eines Magenten bringt, geht die Kraft, die den Nagel anzieht vom Magneten aus. Übermittelt wird die Kraft durch sogenannten Feldlinien, die wir uns als Verständinishilfe vorstellen.
Durch Eisenfeilspäne lassen sich die Feldlinien sichtbar machen. Deutlich erkennbar werden die unten gezeichneten Muster.

Das Magnetfeld eines Stabmagneten:

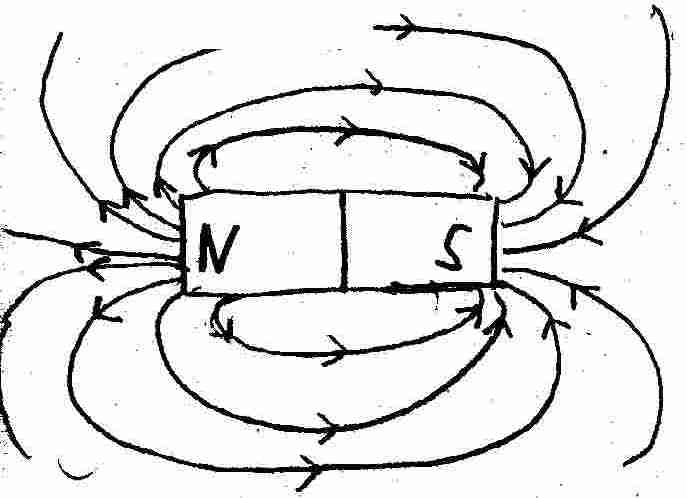
Das Magnetfeld eines Stabmagneten bildet sich wie oben dargestellt aus. Die Richtung des Magnetfeldes lässt sich mit einem kleinen Kompass bestimmen.Die Pfeilspitze wird zum Südpol des Magneten zeigen. Der Kompass wird sich so tangential zu den Feldlinien ausrichten.

Wie sieht das Magnetfeld eines Hufeisenmagneten aus ?


Das Magnetfeld eines Hufeisenmagneten unterteilt sich in 2 Bereiche. Der Teil innerhalb der beiden "Magnetklötzchen" ist das Magnetfeld homogen, außerhalb inhomogen:

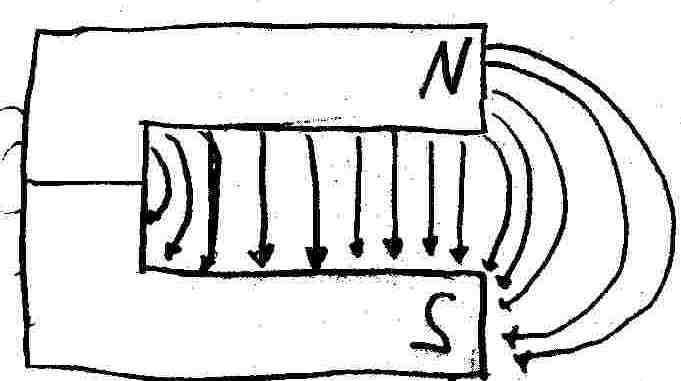
Zusammengefasst:

  • Ähnlich wie bei Ladungen geht man auch bei einem Magneten davon aus, dass er von einem magnetischen Feld umgeben ist.
  • Das magnetische Feld ist Mittler der magnetischen Kräfte.
  • Die magnetischen Feldlinien verlaufen vom Nordpol zum Südpol.
  • Liegen die Feldlinien parallel, so spricht man von einem homogenen Magnetfeld.

Magnetfelder durch Ströme

Während einer Physik-Vorlesung bemerkte der dänische Professor Hans-Christian Oerstedt im Jahre 1820, dass sich zufällig herumstehende Kompassnadeln in der Nähe eines stromdurchflossenen Leiters abgelenkt wurden. So entdeckte er, dass durch Stromfluss um einen Leiter herum ein magnetisches Feld entsteht.

Experiment:
Wir lassen durch einen Draht, der senkrecht zu einer horizontalen Ebene liegt, einen Strom derart fließen, dass die negativen Ladungsträger nach oben fließen. Anschließend streuen wir auf die Ebene Eisenfeilspäne zum Nachweis des magnetischen Feldes. Ergebnis:
Die Eisenfeilspäne bilden ringförmige Muster. Wie in der unteren Abbildung dargestellt, verläuft das Magnetfeld offenbar kreisförmig um den Draht. Ein solches Feld nennen wir magnetisches Wirbelfeld.
Die Richtung des Wirbelfeldes stellen wir mit Kompassnadeln fest: Es verläuft im Uhrzeigersinn. Dreht man die Stromrichtung um, so verläuft es entgegen des Uhrzeigersinns.


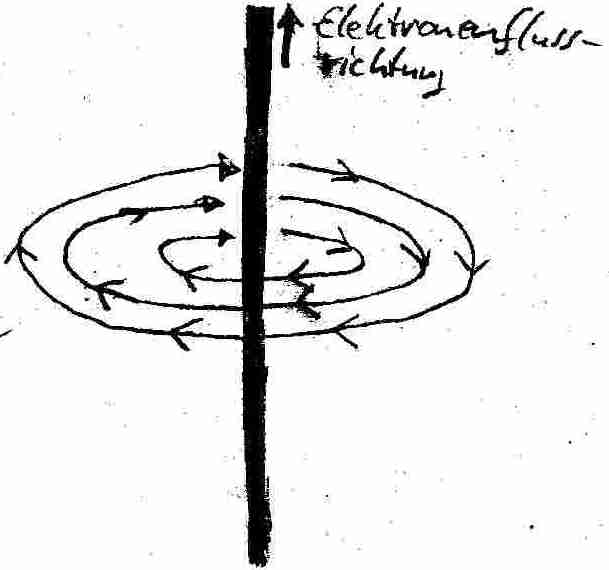
Die Linke-Hand-Regel:
Es ist ganz einfach möglich die Richtung dieses elektrischen Feldes zu bestimmen.
Man nehme die linke Hand und strecke den Daumen in Richtung der Elektronenflussrichtung. Die anderen Finger sollten einen Halbkreis bilden. In Richtung der Fingerspitzen entspricht nun der Richtung der magnetischen Feldlinien.

ACHTUNG: Besonderen Augenmerk muss man auf die technische Stromrichtung haben, denn diese ist der Flussrichtung der Ladungsträger entgegengesetzt.
Dies ist einfach gesichtlich bedingt, als man die Stromrichtung festsetzte, dachte man noch es wären die positiven Ladungsträger, die durch den Leiter fließen. Daher ist die technische Stromrichtung VOM PLUS- ZUM MINUS-POL. Das magnetische Wirbelfeld entsteht aber durch die fließenden Elektronen und daher muss die Flussrichtung der Ladungsträger VOM MINUS- ZUM PLUS-POL beachtet werden. Der Linke Hand Regel gilt also nur, wenn die Flussrichtung der Ladungsträger angegeben ist, oder man muss die Stromrichtung ändern.

Zusammengefasst:

  • Ein stromdurchflossener Draht verursacht ein magnetisches Wirbelfeld.

Das Magnetfeld einer stromdurchflossenen Spule

Das Magnetfeld einer stromdurchflossenen Spule entspricht den überlagerten Feldern der Windungen des gewickelten Drahtes. Es ähnelt äußerlich dem Feld eines Stabmagneten und bildet einen Nordpol dort aus, wo die Feldlinien aus der Spule heraustreten und einen Südpol dort, wo die Feldlinien in die Spule eintreten. Innerhalb der Spule verlaufen die Feldlinien parallel.


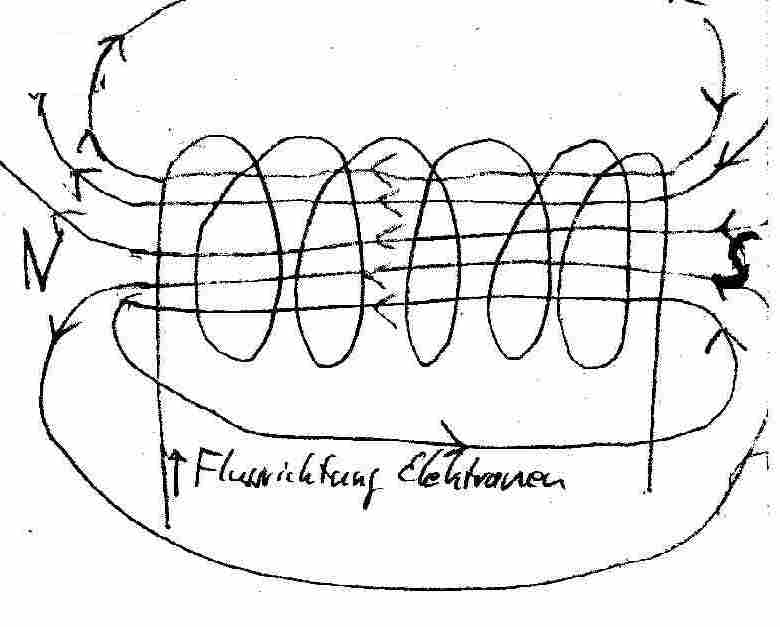
Bereits Andre-Marie Ampere ging davon aus, dass die Elementarmagnete in ferromagnetischen Stoffen nichts anderes sind als Kreisströme, die widerstandsfrei fließen - und damit auch nie aufhören zu fließen.
Tatsächlich verursachen die Bahnbewegungen der Elektronen um die Atomkerne Magnetfelder. Die Elementarmagnete "entstehen" aber vor allem durch die "Rotation" der Elektronen um die eigene Achse.

Zusammengefasst:

  • Das Magnetfeld einer stromdurchflossenen Spule ähnelt äußerlich dem Magnetfeld eines Stabmagneten.
  • Im Innern einer lang-gestreckten Spule ist das Magnetfeld homogen.

Die Lorentzkraft

Die Pole eines Magneten ziehen keine Ladungen an, denn ansonsten wären sie geladen. Doch beeinflussen magnetische Felder überhaupt Ladungen?
Um diese Frage zu beantworten, untersuchen wir mithilfe einer "Elektronenkanone" die Flugbahn von Elektronen, wenn dir die Elektronenröhre mit einem Magnetfeld durchsetzen.

Experiment:
Mithilfe einer "Elektronenkanone" kann man Elektronenstrahlen erzeugen und deren Verlauf beobachten. In der Abbildung ist das Ergebnis dargestellt; Das Magnetfeld verläuft in der Abbildung in die Zeichenebene hinein.

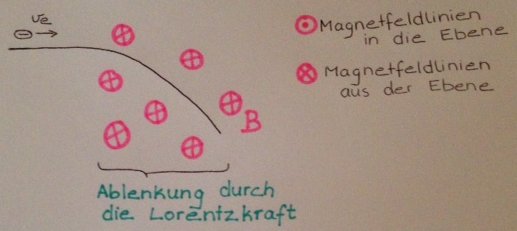
Ergebnis:
Das Magnetfeld bewirkt auf bewegte Ladung eine Kraft, die sowohl senkrecht zur Bewegungsrichtung v der Elektronen, als auch senkrecht zu den Magnetfeldlinien wirkt. Diese Kraft wird Lorentzkraft genannt und bewirkt die Ablenkung des Elektronenstrahls im Magnetfeld.

Zusammengefasst:

  • Schickt man einen Elektronenstrahl durch ein Magnetfeld, so wird er senkrecht zur Bewegungsrichtung und senkrecht zum magnetischen Feld abgelenkt.
  • Die ablenkende Kraft nennt man Lorentzkraft.

Kraft auf stromdurchflossene Leiter

Magnetische Felder bewirken auf sich in einem Elektronenstrahl bewegende Elektronen eine Kraft, die wir Lorentzkraft genannt haben. Lassen sich ähnliche Kräfte auch bei bewegten Ladungen während des Stromflusses in Stromleitungen beobachten?

Experiment:
Wir lassen durch ein leicht biegbares Metallband aus einem Kupferdrahtgeflecht einen Strom fließen und führen diese stromdurchflossene Leitung in ein Magnetfeld.

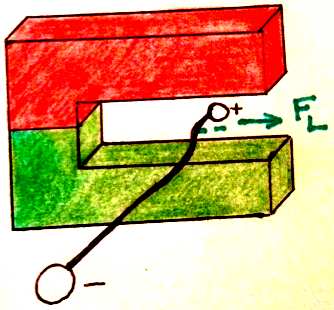
Beobachtung und Ergebnis:

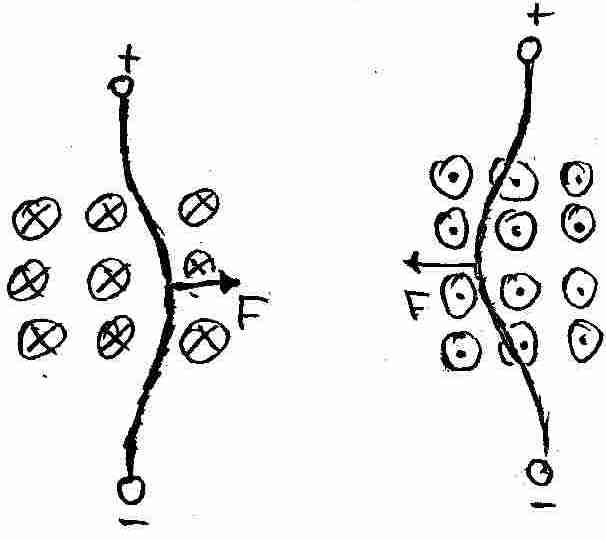
Man beobachtet,wie sich der Leiter senkrecht zum Magnetfeld und senkrecht zu der Bewegungsrichtung der Elektronen auslenkt. Offenbar erfahren die fließenden Elektronen im Leiter die Lorentzkraft und übertragen diese Kraft auf den Leiter.

Mithilfe von Magnetfeldern lassen sich also auf einfache Weise durch elektrische Ströme mechanische Kräfte verursachen. Man nutzt diesen Effekt bei Elektromotoren, die auf diesem Prinzip basieren.

Zusammengefasst:

  • Lorentzkräfte wirken auch dann, wenn sich Elektronen innerhalb von elektrischen Leitern durch Magnetfelder bewegen.
  • Die zu beobachtende Kraft wirkt auch hier senkrecht zur Bewegungsrichtung der Elektronen und senkrecht zum Magnetfeld.

Die magnetische Flussdichte - ein Maß für die Stärke magnetischer Felder

Wovon hängt die Größe der Kraft F auf einem stromdurchflossenen Leiter im Magnetfeld ab?

Sicher von der Stromstärke und der Leiterlänge im magnetichen Feld. Aber sicher auch von der "Stärke" des Magnetfeldes, die sich daher mithilfe dieser Kraft definieren lässt.

Experiment:
Ein rechteckiger, stromdurchflossener Drahtrahmen befindet sich im Magnetfeld (vgl. Abbildung). Da sich die Kräfte F1 und F2 ausgleichen, kann nur F gemessen werden.

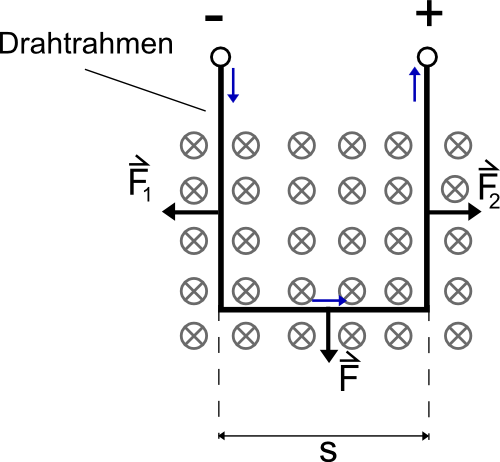
Ergebnis:
Die Kraft ist proportional zum Strom I und zur Drahtlänge s:

Das heißt, der Ausdruck
ist so lange konstant, wie wir die Stärke des magnetischen Feldes konstant halten. Damit definieren wir als Maß für die Stärke des Magnetfeldes die Größe B:

Die Einheit für B nennt sich Tesla. Ihre Definition ergibt sich aus der obigen Gleichung für B:

B wird die magnetische Flussdichte genannt. Sie lässt sich mit sogennanten Hallsonden leicht messen.

Schlussfolgerung: Die Kraft auf einen Leiter der Länge s, welcher sich im Magnetfeld mit der Flussdichte B befindet und durch den der Strom I fließt, beträgt:

wenn das Magnetfeld senkrecht zum Leiter verläuft.

Zusammengefasst:

  • Die magnetische Flussdichte B ist ein Maß für die Stärke eines Magnetfelds.
  • Befindet sich ein Leiter mit der Länge s senkrecht zu einem Magnetfeld der Flussdichte B und wird er vom Strom I durchflossen, so wirkt senkrecht zum Magnetfeld eine Kraft mit dem Betrag

Die Lorentzkraft berechnen

Der Strom I durch einen Leiter entsteht durch die durch den Leiter fließenden Elektronen. Die Kraft

auf diesen Leiter im Magnetfeld setzt sich also aus der Summe der Kräfte auf die einzelnen fließenden Elektronen zusammen. Wir werden diese Formel jetzt nutzen, um eine Formel für die Kraft auf ein einzelnes Elektron, welches sich mit der Geschwindigkeit v_e durch ein Magnetfeld bewegt, herzuleiten. Dazu betrachten wir zunächst die Gesamtheit der Elektronen, die aufgrund ihrer Bewegung mit der Geschwindigkeit v_e den Strom durch den Draht verursachen: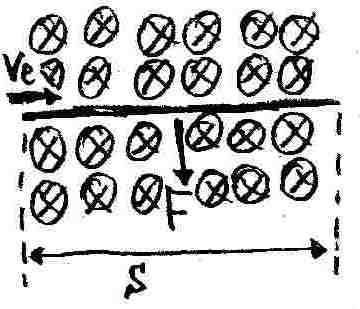

Bewegt sich ein Elektron die Strecke s entlang des Leiters und benötigt dazu die Zeit t, so ist seine Geschwindigkeit

Angenommen, der Leiter hat auf dieser Strecke N sich bewegende Elektronen. Dann bewegen sich durch eine Querschnittsfläche des Leiters in dieser Zeit t insgesamt N Elektronen mit der Gesamtladung

, wobei
die Elementarladung ist. Der Strom I lässt sich aus diesem Grund wie folgt schreiben:
Die N Elektronen bewirken somit die Kraft
Die Lorentzkraft ist nun die Kraft auf ein einzelnes Elektron. Wir müssen zu ihrer Berechnung die Formel für die Kraft auf N Elektronen durch die Anzahl N teilen:

Allgemein gilt: Bewegt sich ein Körper mit der Ladung q und der Geschwindigkeit v durch ein Magnetfeld, so wirkt auf ihn die Kraft

Zusammengefasst:

  • Ein Körper der Ladung q bewegt sich mit der Geschwindigkeit v senkrecht zu einem Magnetfeld der Flussdichte B. Dann wirkt senkrecht zur Bewegungsrichtung und senkrecht zum Feld die Lorentzkraft
    auf das Teilchen.

Das Magnetfeld einer lang gestreckten Spule

Die Stärke des Magnetfeldes im Innern einer lang-gestreckten Spule hängt vermutlich ab von:

  • der Stromstärke I
  • der Windungsdichte N/l (Anzahl Windungen pro Meter)

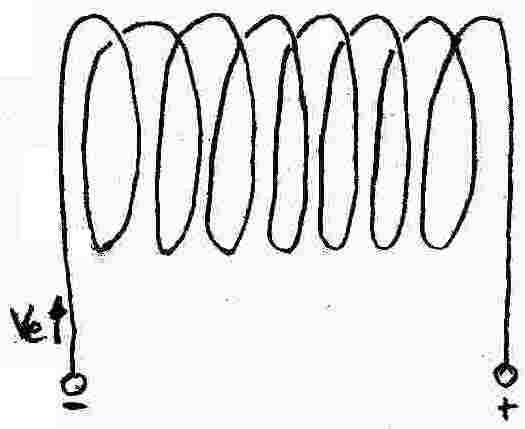
Diese Vermutungen lassen sich experimentell durch Spulen verschiedener Bauart bestätigen. Es lässt sich auch experimentell darstellen, dass B im Innern der Spule nicht vom Spulendurchmesser oder von der Länge l der Spule abhängt, wenn obige Größen konstant bleiben.

Vermutung über den quantitativen Zusammenhang:

mit der Proportionalitätskonstanten

==> Exp.: Die Formel wird durch Messungen an verschiedenen Spulen bestätigt. Die Proportionalistätskonstante kann aus den Messwerten bestimmt werden:

Man nennt sie magnetische Feldkonstante.

==> Exp.: Steckt man in die Spule einen ferromagnetischen Stoff, so verstärkt sich die Flussdichte um einen Faktor my_r. my_r ist eine Materialkonstante und wird Permeabilitätszahl gennant.
Mit ihr gilt für die magnetische Flussdichte im Innern einer lang gestreckten Spulen:

Zusammengefasst:

  • Fließt der Strom I durch eine lang gestreckte Spule der Länge l und mit N Windungen, so lässt sich die magnetische Flussdichte im Innern der Spule berechnen zu
  • Die Konstante
    ist eine Naturkonstante und heißt magnetische Feldkonstante.
  • Schiebt man einen ferromagnetischen Stoff in die Spule, so verstärkt sich das Magnetfeld in dessen Innern um einen materialabhängigen Faktor my_r. Dieser wird Permeabilitätszahl genannt.

Bestimmung der Masse von Elektronen

Bisher haben wir in diesem Skript die Kenntnis von der Masse und der Ladung der Elektronen vorrausgesetzt. In diesem Abschnitt wird gezeigt, wie die Elektronenmasse "gemessen" werden kann. Die Massenbestimmung ist mit einem sogenannten Fadenstrahlrohr möglich:

72.1Aufbau des Fadenstrahlrohrs

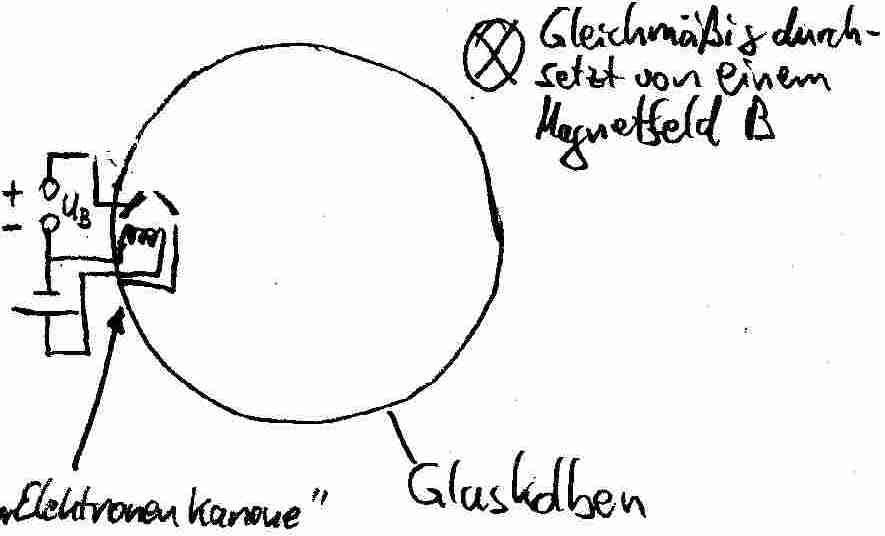
Das Fadenstrahlrohr besteht aus einem kugelförmigen Glaskolben, in dessem Inneren eine Elektronenröhre (="Elektronenkanone") befestigt ist. Der Kolben wird von einem homogenen Magnetfeld durchsetzt, welches durch ein so genanntes Helmholtz-Spulenpaar erzeugt wird.

72.2 Geltende Zusammenhänge

Schaltet man die Elektronenröhre an, so sieht man durch fluoreszierende Gase in dem Glaskolben, dass die Elektronen auf einer Kreisbahn fliegen. Den Radius der Bahn r kann an einer Skala abgelesen werden.

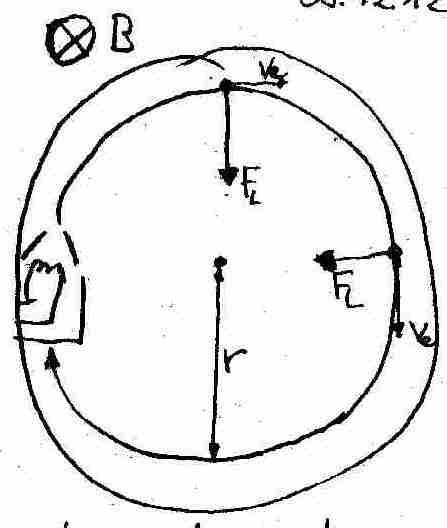
Doch wie kommt diese Kreisbahn zustande?

  • Durch die Beschleunigungsspannung UB werden die Elektronen mit der Energie
    beschleunigt, wodurch diese Energie in kinetische Energie umgewandelt wird.
  • Im Magnetfeld wirkt die Lorentzkraft stehts senkrecht zum Feld und zur Bewegungsrichtung des Elektrons:
  • FL zwingt die Elektronen auf eine Kreisbahn. Sie entspricht also der Zentripetalkraft einer Kreisbewegung. Folgende Formel für Zentripetalkräfte kennen wir aus der Mittelstufe:

72.3 Bestimmung der Masse me eines Elektrons

Im nächsten Abschnitt wird die Elektronenladung e bestimmt. Sie beträgt:

Messbare Größen bei diesem Experiment sind: r, UB und B
Nun entspricht die Zentripetalkraft der Lorentzkraft, woraus folgt:

Wir können die zugehörigen Gleichungen direkt einsetzen und erhalten

Die Geschwindigkeit kann man wegkürzen:
Um me zu bestimmen, setzen wir in diese Gleichung die in vorherigen Abschnitten hergeleitete Formel für die Geschwindigkeit der mit UB beschleunigten Elektronen

ein...

Quadrieren und kürzen ergibt

woraus durch Umstellen für me folgt:

Setzen wir die gemessenen Größen ein, erhalten wir die Elektronenmasse. Literaturwert:

Zusammengefasst:

  • Bewegen sich mit der Beschleunigungsspannung UB beschleunigte Elektronen im vom Magnetfeld der Flussdichte B durchdrungenen Fadenstrahlrohr auf einer Bahn mit Radius r, so lässt sich das Verhältnis aus Elektronenmasse zu Elektronenladung bestimmen

Der Massenspektrograph

Mit einem Massenspektrograph werden die Massen von Molekülen und Atomen, beispielsweise zur Analyse von Lebensmitteln, bestimmt. Er besteht aus einem Wien'schen Geschwindigkeitsfilter, welcher nur Teilchen einer bestimmten Geschwindigkeit hindurch lässt, einem magnetischen Ablenkfeld und einer Fotoplatte.

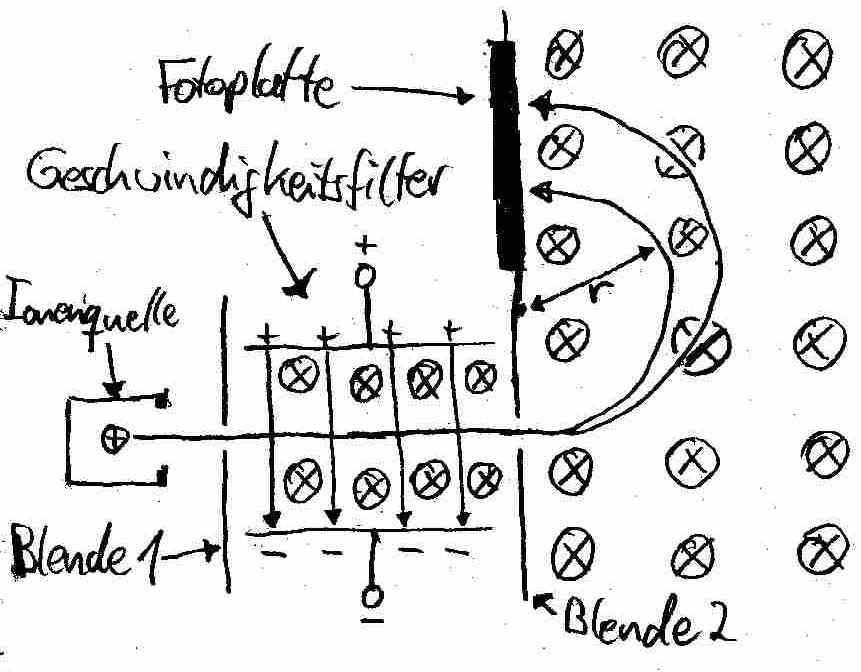
Im Folgenden gehen wir jetzt auf die Bestandteile genauer ein und nehmen dabei Bezug auf die obige Abbildung.

74.1 Prinzip des magnetischen Ablenkfeldes

Durch Blende 2 gelangen die unterschiedlich massereichen Ionen mit gleicher Geschwindigkeit v in das magnetische Ablenkfeld. Hier entspricht die Lorentzkraft der Zentripetalkraft der Kreisbewegung der Teilchen mit Radius r:

Löst man nach m auf, erhält man für die Masse der Teilchen:

Die Stärke des B-Feldes lässt sich mit Hall-Sonden messen, der Radius r kann man über die Einschlagstelle auf der Fotoplatte bestimmen, die Geschwindigkeit v kann über den Geschwindigkeitsfilter eingestellt werden und q kann als Vielfaches der Elementarladung durch logische Schlüsse ermittelt werden. Damit sind alle Größen zur Brechnung von m bekannt.
Voraussetzung war aber, dass alle Ionen mit der gleichen Geschwindigkeit die Blende 2 passieren. Dies stellt man mit dem sogenannten Wien'schen Geschwindigkeitsfilter sicher.

74.2 Der Wien'sche Geschwindigkeitsfilter

Der Geschwindigkeitsfilter besteht aus einem senkrecht gekreuzten, magnetischen und elektrischen Feld. Auf die positiv geladenen Ionen wirken beim Durchfliegen des Filters zwei Kräfte: Eine geschwindigkeitsunabhängige Kraft durch das elektrische Feld E, die in der obigen Abbildung nach unten wirkt:

Und eine geschwindigkeitsabhängige Kraft durch das magnetische Feld B, die in der Abbildung nach oben wirkt:
Den Geschwindigkeitsfilter können aufgrund der Blenden nur jene Teilchen passieren, die genau geradeaus fliegen. Das ist aber nur der Fall, wenn sich die nach oben wirkende Kraft FL und die nach unten wirkende Kraft FE gerade aufheben:

Für v folgt daraus:

Nur Teilchen mit dieser Geschwindigkeit werden durchgelassen. Bleibt B konstant, kann man wegen E = U/d bestimmte Geschwindigkeiten durch anlegen der passenden Spannung U auswählen:

Zusammengefasst:

  • Ist die Ladung q von Teilchen unbekannter Masse bestimmen, so lässt sich die Masse über ein Massenspektrographen berechnen
  • Der Wien'sche Geschwindigkeitsfilter besteht aus einem gekreuzten magnetischen Feld B und elektrischem Feld E. Er lässt nur die Teilchen durch, die die folgende Geschwindigkeit besitzen:

Der Halleffekt

75.1
Der Hall-Effekt kann dazu genutzt werden, auf einfache Weise die magnetische Flussdichte an Magnetfeldern zu messen. Er lässt sich anhand des stark vergrößert dargestellten Metallblättchens erklären:

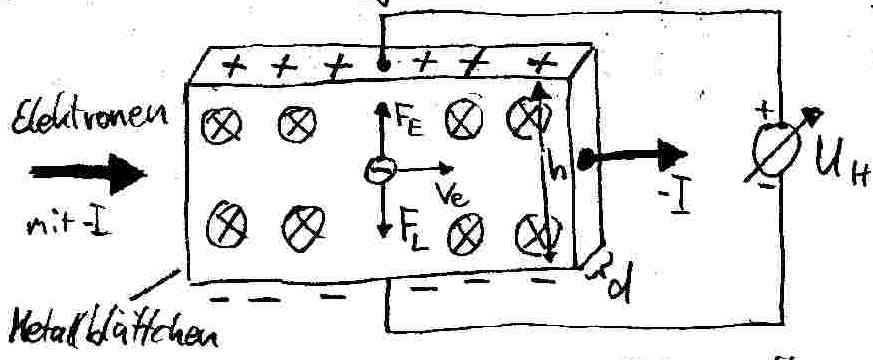
Es wird, wie dargestellt, von Elektronen durchflossen. Senkrecht zum Elektronenfluss wird es von einem Magnetfeld durchsetzt. Bewegen sich die Elektronen mit der Geschwindigkeit ve nach rechts, so erfahren sie die nach unten gerichtete Lorentzkraft FL. Dadurch sammeln sie sich an der unteren Seite des Blättchens. Dort gibt es einen Elektronenüberschuss, während an der Oberseite ein Elektronenmangel entsteht. Die so entstandene Spannung UH lässt sich messen.

Wir werden für diese Spannung jetzt eine Formel herleiten:
Fasst man die obere und die untere Fläche Blättchen als Kondensatorplatten auf, kann man daraus die Feldstärke

berechnen, die durch die positiven Ladungen auf der oberen Fläche und durch die negativen Ladungen auf der unteren Fläche erzeugt wird. Diese bewirkt aber eine nach oben gerichtete elektrische Kraft
auf die Elektronen. Wenn FE so groß geworden ist, dass sie FL ausgleicht, steigt die Spannung UH nicht weiter an. Sie hat ihren Maximalwert erreicht. Es gilt dann:

woraus durch Einsetzen folgt

Durch Umstellen nach UH erhalten wir schließlich die Formel für unsere Hallspannung:

Bei einer Hall-Sonde nimmt man ein Metall mit bekannter Driftgeschwindigkeit ve und errechnet mithilfe der gemessenen Hallspannung die magnetische Flussdichte:

Bei bekanntem B-Feld lässt sich umgekehrt die Driftgeschwindigkeit der Elektronen ve berechnen.

75.2 Die Hall-Spannung in Abhängigkeit zur Dichte der Leitungselektronen

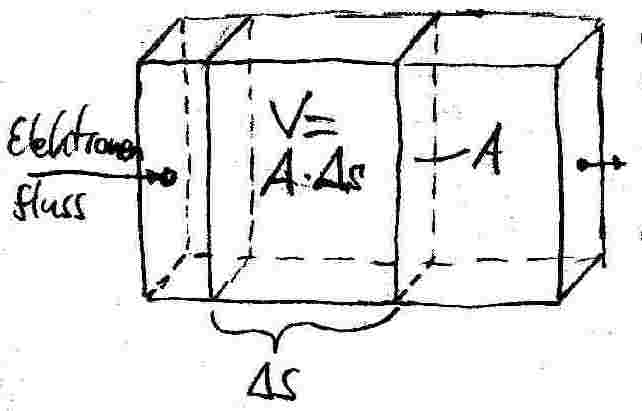
Wir betrachten nun das eingezeichnetet Volumen V des Leiterblättchens. N sei die Anzahl der Leitungselektronen in diesem Volumen. Mit der Driftgeschwindigkeit der Elektronen

lässt sich der Strom I dann wie folgt ausdrücken:

Die Anzahldichte der Leitungselektronen ist als Anzahl Elektronen pro Volumen definiert:

Diesen Ausdruck für N können wir in die obige Formel für die Stromstärke einsetzen.

Daraus folgt für die Driftgeschwindigkeit der Elektronen

Setzen wir diese Formel in die Hallspannung ein, erhalten wir:

Dies ist die Formel der Hallspannung in Abhängigkeit zur Dichte der Leitungselektronen. Mit ihr lässt sich die Anzahl der Elektronen pro Volumen durch Umstellen bestimmen:

Durch Einsetzen der Elektronenzahldichte in die obige Formel für die Driftgeschwindigkeit können wir ausrechnen, mit welcher Geschwindigkeit sich die Elektronen durch das Metall bewegen, wenn ein Strom fließt.

Zusammengefasst:

  • Mit dem Hall-Effekt wird die magnetfeldbedingte Ablenkung von Elektronen in einem Metall beschrieben.
  • Jenachdem, welche Größe bekannt ist, kann man mit dem Hall-Effekt...
    • ... die Driftgeschwindigkeit von Elektronen in Metallen messen.
    • ... die Elektronendichte in Metallen messen.
    • ... die magnetische Flussdichte B bestimmen.