Homogene elektrische Felder und der Zusammenhang mit Ladungen
- Faraday's Feldtheorie
- Feldlinienbilder von Punktladungen und Kondensatoren
- Elektrische Kräfte wirken tangential zu den Feldlinien
- Der Faraday'sche Käfig
- Der Zusammmenhang zwischen Ladung, Kraft und Stärke des E-Feldes
- Parallelen und Unterschiede zwischen elektrischem Feld und Gravitation
- Elektrische Arbeit und Bewegungen senkrecht und diagonal zu den Feldlinien
- Definition der Spannung
- Untersuchung der Spannung zwischen Kondensatorplatten
- Potential und Äquipotentialfläche
- Der Zusammenhand zwischen U, E und d beim Plattenkondensator
- Der Zusammenhang zwischen Flächenladung und Feldstärke
- Die Flächenladung hängt tatsächlich nur vom Feld E ab!!
- Die Flächenladungsdichte
- Der Zusammenhang zwischen Flächenladungsdichte und Feldstärke
- Die Kapazität eines Kondensators
- Die Dieelektrizitätszahl
- Mikroskopische Betrachtung von Isolatoren in elektrischen Feldern
- Die in Kondensatoren gespeicherte Energie
- Die Energiedichte des elektrischen Feldes
- Die Elektronenkanone
- Die Einheit Elektronenvolt
- Das Ablenksystem einer Brown'schen Röhre
Faraday's Feldtheorie
In den vorhergehenden Abschnitten stellten wir fest, dass gleichnamige elektrische Ladungen sich abstoßen, während ungleichnamige sich anziehen. Doch wo rühren diese Kräfte her?
- Früher glaubte man an Fernkräfte, die den Raum instantan durchdringen.
- Faraday nahm an, dass der Raum um Ladungen herum durch ein elektrisches Feld durchzogen wird, welches die Kräfte vermittelt.
- Dieses Feld lässt sich mit sogenannten Feldlinien zeichnerisch darstellen.
- Ladungen erfahren in solchen elektrischen Feldern Kräfte, die tangential zu den Feldlinien wirken:
Im Laufe der Zeit stellte sich heraus, dass diese Feldvorstellung richtig zu sein scheint. Wir werden im Laufe dieses Kurses selbst immer weitere Indizien dafür sammeln.
Zusammengefasst:
- Ladungen sind von einem elektrischen Feld umgeben.
- Dieses Feld ist Mittler der elektrischen Kräfte.
Feldlinienbilder von Punktladungen und Kondensatoren
Experiment: Wir geben einige Grieskörner in eine Schale mit Rizinusöl. In das Öl tauchen wir Metallstempel, die wir unterschiedlich aufladen können. Laden wir sie auf, werden in den Grieskörnern Dipole induziert, welche sich entlang der elektrischen Feldlinien ausrichten. Wir untersuchen somit den Verlauf des Feldes bei folgenden Körpern:
Das Feld einer Punktladung:
Das Feld zweier sich anziehender Punktladungen:
Das Feld zweier sich abstoßender Punktladungen:
Das Feld eines Kondensators:
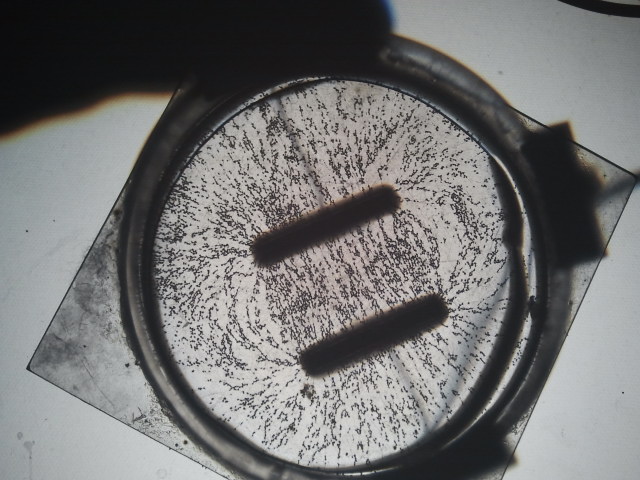
Zwischen zwei Kondensatorplatten verlaufen die Feldlinien parallel und im gleichen Abstand. Überall ist die Stärke des elektrischen Feldes gleich groß. Solche Felder nennt man homogen.
Zusammengefasst:
- Das elektrische Feld einer Punktladung verläuft radial nach außen.
- Die Feldlinien zwischen Kondensatorplatten verlaufen parallel. Man nennt diese Felder homogen.
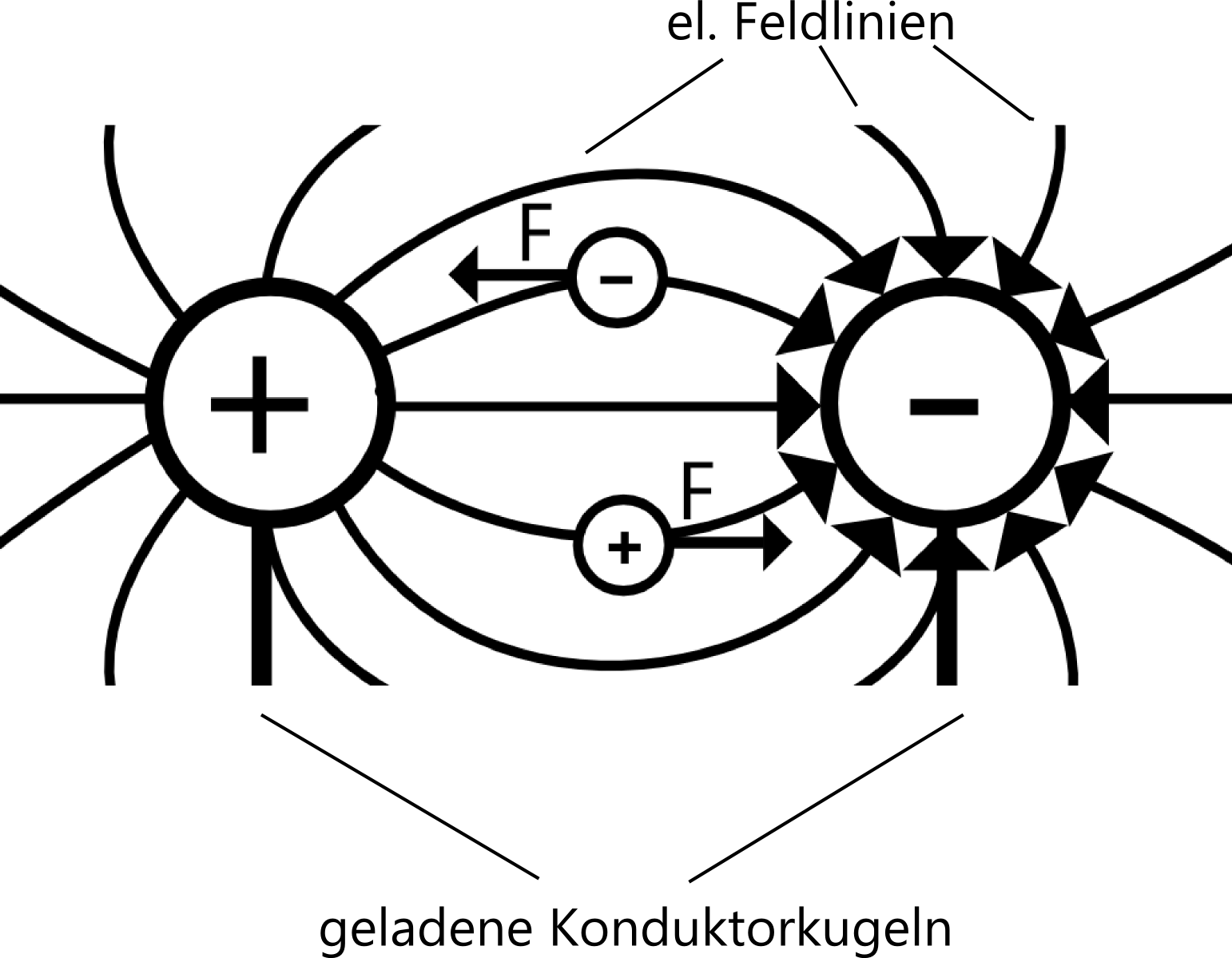
Elektrische Kräfte wirken tangential zu den Feldlinien
Experiment:
Eine kleine gelandene Konduktorkugel wird an einem isolierten Faden in den Kondensator gehalten
Beobachtung:
Die Kugel schlägt parallel zur E-Feld-Richtung aus, wenn sie positiv gelanden ist. Bei negativer Ladung schlägt sie antiparallel zur E-Feld-Richtung aus.
Hieraus können wir schlussfolgern:
Elektrische Kräfte wirken tangential zu den Feldlinien (F II E-Feld)
Zusammengefasst:
- Elektrische Kräfte wirken immer tangential zu den Feldlinien.
Der Faraday'sche Käfig
Der Faraday'sche Käfig ist ein Begriff, der in vielen Bereichen des Alltags einzug gehalten hat. Aber was steckt eigentlich dahinter?
Um das zu ergründen, sehen wir uns an, was passiert, wenn man einen Metallring in ein elektrisches Feld gibt:
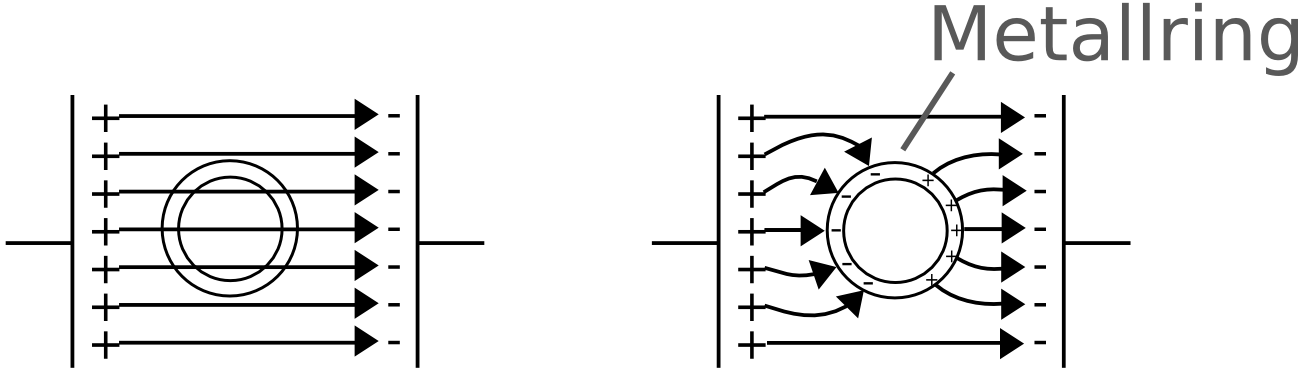
Links in der Abbildung sehen wir den vom elektrischen Feld durchsetzten Ring. Die negativen Ladungen in Metallen sind aber beweglich. Das äußere Feld bewirkt eine Kraft auf die beweglichen Ladungen und sorgen für eine Ladungsverschiebung im Ring.
Dieser Zustand ist rechts eingezeichnet. Dadurch, dass sich die Ladungen innerhalb des Rings verschieben, erzeugen sie ein Gegenfeld zum äußeren Feld. Das elektrische Feld im Innern des Rings wird mit der zunehmenden Ladungsverschiebung zunehmend abgeschwächt, bis es verschwunden ist. In diesem Gleichgewichtszustand sind die Ladungen verschoben, und das Innere des Rings ist feldfrei.
Ein Faraday'scher Käfig ist also gewissermaßen ein feldfreier Raum. Lebewesen sind in solchen feldfreien Räumen vor elektrischen Übersprüngen wie Blitze geschützt.
Zusammengefasst:
- Das Innere eines Faraday'schen Käfigs ist feldfrei.
Der Zusammmenhang zwischen Ladung, Kraft und Stärke des E-Feldes
Wovon hängt die Stärke der auf die Ladung q wirkende elektrischen Kraft F ab?
Vermutlich von der Menge an Ladung q, auf die die Kraft wirkt. Vermutlich aber auch von etwas, was man die "Stärke" des elektrischen Feldes bezeichnen könnte: Die elektrische Feldstärke kürzen wir mit dem Buchstaben E ab.
Wir vermutend die folgenden Zusammenhänge:
- Je größer die Ladung q, desto größer die elektrische Kraft F
- Je größer die Feldstärke E, desto größer die elektrische Kraft F
Wir prüfen unsere Vermutungen anhand eines Experiments.
Experiment:
Eine Konduktorkugel wird an einen digitalen, sehr genauen Kraftmesser befestigt. Wir lasen sie positiv auf, bringen sie in ein elektrisches Feld und messen die durch das Feld verursachte elektrische Kraft auf die Ladung.
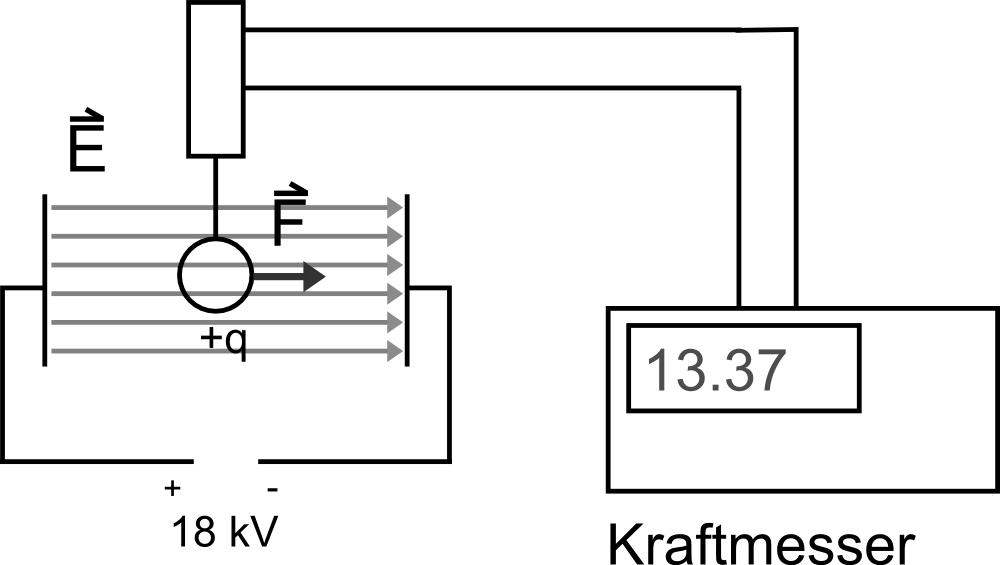Beobachtung:
- Verdoppeln wir die Ladung auf der Konduktorkugel, so verdoppelt sich auch die auf sie wirkende Kraft F.
- Verdoppeln wir die Stärke des elektrischen Feldes (durch Erhöhung der Spannung am Kondensator), so verdoppelt sich die Kraft F.
Ergebnis:
Die oben genannten Vermutungen werden durch das Experiment bestätigt.
Mathematisch können wir für den Zusammenhang zwischen Kraft, Ladung und Feldstärke den folgenden Zusammenhang ansetzen:
Die Formel beschreibt den beobachteten Zusammenhang richtig: Verdoppelt man die Ladung bei gleicher Feldstärke, so verdoppelt sich - auch nach der Formel - die Kraft. Analog beschreibt die Formel auch die Kraft bei Verdopplung der Feldstärke richtig.
Streng genommen wäre es möglich, dass sich die Kraft um einen konstanten Vorfaktor von q*E unterscheidet. Allerdings hatten wir E bisher noch nicht mathematisch definiert - und können es so definieren, dass obige Gleichung auch ohne Vorfaktor gilt:
Definition:
Die Feldstärke E in einem Punkt des Feldes ist der von der Ladung q unabhängige Vektor
Die Pfeile über E und F symbolisieren, dass es sich bei der Feldstärke und der Kraft um gerichtete Größen handelt: Sowohl die Feldstärke als auch die Kraft wirken in eine bestimmte Richtung. Dies wird durch die Pfeile angedeutet.
Zusammengefasst:
- Die Stärke eines elektrischen Feldes wird als elektrische Feldstärke E bezeichnet. Sie hat die Bedeutung von Kraft pro Ladung.
- Die Kraft F auf eine Ladung q im Feld der Stärke E lässt sich berechnen durch
Parallelen und Unterschiede zwischen elektrischem Feld und Gravitation
In diesem Abschnitt werden die Eigenschaften elektrischer Kräfte mit den Gravitationskräften aus der Mittelstufe verglichen:
Analogien:
| Feldart | gravitativ | elektrisch |
|---|---|---|
| Eigenschaft des Probekörpers | Masse m | Ladung |
| Kräfte | ||
| Feldstärke | ||
| Arbeit bei Strecke d parallel zum Feld | => im homogenen Feld |
Unterschiede:
- Das Gravtiationsfeld wirkt auf Massen, das E-Feld auf Ladungen
- Gravitationskräfte wirken nur anziehend, elektrische Kräfte können zudem auch abstoßend wirken
- Es gibt nur eine "Art" der Masse, aber zwei "Arten" an Ladungen: Positive und negative Ladungen
Elektrische Arbeit und Bewegungen senkrecht und diagonal zu den Feldlinien
Welche Arbeit wird verrichtete, wenn man eine Ladung q parallel zu den Feldlinien verschiebt?
Die mechanische Arbeit W ist definiert als Kraft (Formelzeichen F) mal Weg (Formelzeichen d):
Setzen wir für F die Formel für die elektrische Kraft ein, erhalten wir:
Dies ist die verrichtende Arbeit, wenn eine Ladung q entlang der Feldlinien des Feldes der Stärke E um die Strecke d verschoben wird.
Doch: Welche Arbeit wird verrichtet, wenn wir die Ladung senkrecht oder diagonal zu den Feldlinien verschieben?
Diese Frage können wir leicht beantworten, wenn wir die Analogie zum Gravitationsfeld nutzen:
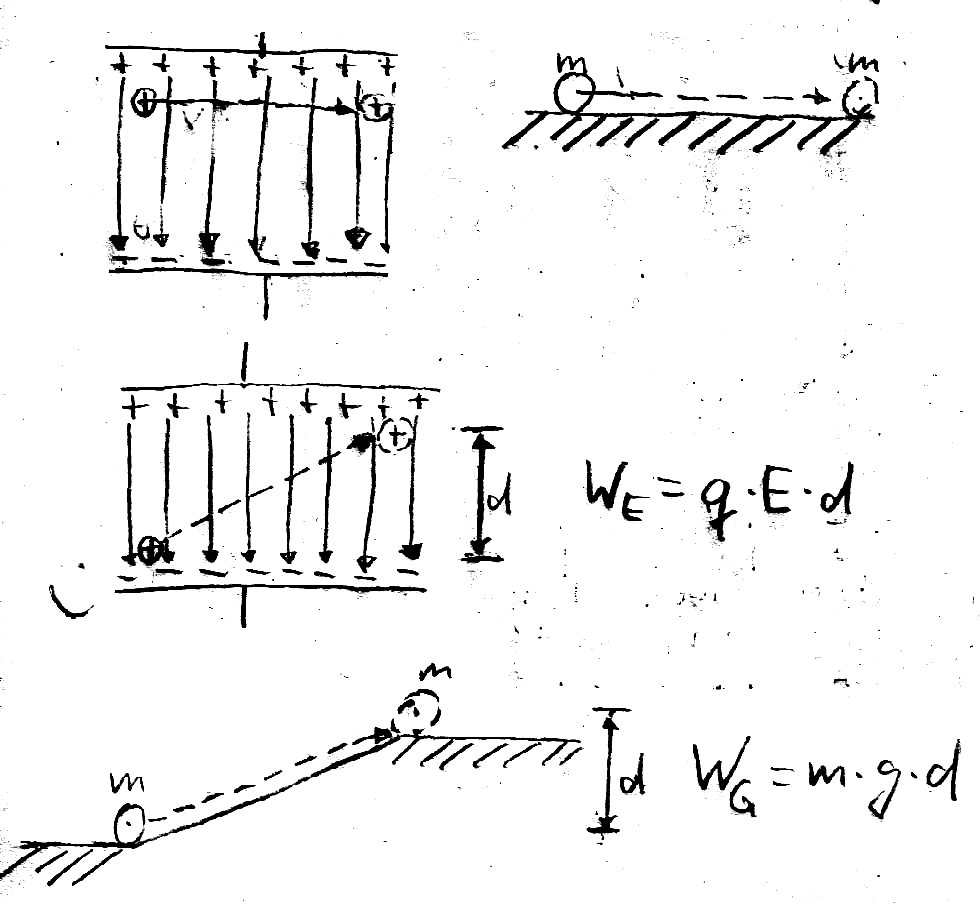
1. Bildreihe: Wie bei der Gravitation bei Massen auch, wird keine Arbeit durch das Feld verrichtet wenn sich die Ladungen senkrecht zu den Feldlinien bewegen, da hierzu keine zusätzliche Kraft benötigt wird.
2. Bildreihe: Wie bei der Gravitation, hängt die Transportarbeit nur von dem Anteil "d" der Strecke ab, der in Richtung der Feldkräfte verläuft. Damit muss nur der Anteil der zurückgelegten Strecke berücksichtigt werden, der in Richtung der Feldlinien verläuft.
Zusammengefasst:
- Zur Berechnung der Transportarbeit einer Ladung durch ein elektrisches Feld muss nur der Anteil des zurückgelegten Weges berücksichtigt werden, der parallel zu den Feldlinien ist.
Definition der Spannung
Feldlinien verrichten an der Ladung q zwischen zwei Punkten im elektrischen Feld die Transportarbeit W. Die elektrische Spannung zwischen diesen Punkten ist dann wie folgt definiert:
Als Spannung bezeichnet man in der Physik als nichts anderes als Arbeit pro Ladung. Sie hat das Formelzeichen U; mit ihm drückt sich der Zusammenhang durch folgende Formel aus:
Die Einheit der Spannung ist das Volt. Ein Volt setzt sich aus den Einheiten Joule (für Arbeit) und Coulomb (für Ladung) zusammen.
Beispiel: Die Spannung 1V bedeutet also, dass beim Transport der Ladung 1C von den Feldkräften die Arbeit 1J verrichtet wird.
Zusammengefasst:
- Die Spannung zwischen zwei Punkten ist definiert als die Arbeit, die pro Ladung benötigt wird, um eine Ladung von dem einen Punkt zum anderen Punkt zu transportieren.
- Die Einheit der Spannung ist das Volt.
Untersuchung der Spannung zwischen Kondensatorplatten
Exp.: Zwischen zwei Aluminiumstreifen, welche die Kondesatorplatten darstellen, wird ein feuchtes Papiertuch gelegt. Die "Platten" werden mit einem Netzgerät auf die Spannung 9 Volt gebracht. Das Ganze wird zur Abschirmung von außen auf eine Styroporplatte gelegt. Mit einem Messverstärker können nun die Spannungsdifferenzen zwischen zwei beliebigen Punkten zwischen den Platten gemessen werden.
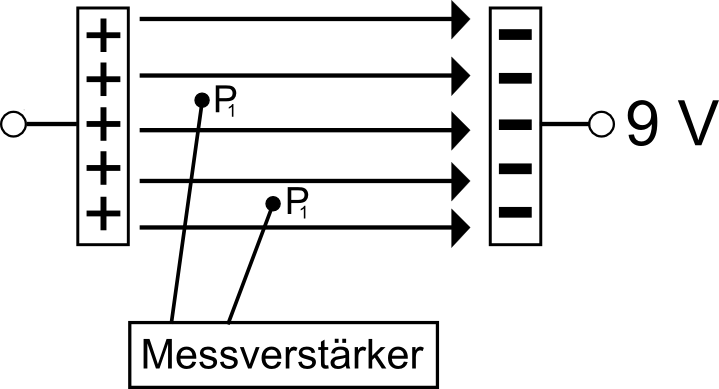
Feststellungen:
- Zwischen zwei Punkten, die auf einer Parallelen zu den Kondensatorplatten liegen, ist die Spannung Null.
- Die Spannung nimmt parallel zu den Feldlienien linear zu.
=> Spannung existiert in einem Feld auch dann, wenn keine Ladungen transportiert werden. Sie gibt die Arbeit pro Ladung an, die ein Feld verrichten würde, wenn sich die Ladung von dem einen zum anderen Punkt bewegen würde.
Zusammengefasst:
- Die Spannung ist eine Zustandsgröße. Sie existiert auch dann, wenn keine Ladung transportiert wird.
- Im Feld eines Plattenkondensators ist die Spannung zwischen zwei Punkten, die auf einer Parallelen zu den Platten liegen, Null.
- Die Spannung nimmt im homogenen Feld parallel zu den Feldlinien linear zu.
Potential und Äquipotentialfläche
Mithilfe flexibler Drähte tasten wir das elektrische Feld zwischen zwei Kondensatorplatten ab und bestimmen die Spannung zwischen den beiden Messpunkten P_1 und P_2:
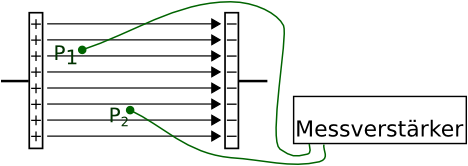
In Anlehnung an den Begriff der potentiellen Energie aus der Mechanik, führen wir jetzt den Begriff des elektrischen Potentials ein:
Die Spannung relativ zur zu einem feststehenden Bezugspunkt, nennen wir elektrisches Potential. Dieser Bezugspunkt wird Nullpunkt des Potentials genannt und kann beliebig festgelegt werden: Legt man beispielsweise die linke Kondensatorplatte in der obigen Abbildung als Nullpunkt des Potentials fest, so ist das Potential des Punktes P_1 nichts anderes als die Spannung zwischen der linken Platte und dem Punkt P_1. Das Potential im Punkt P_2 ist wiederum nichts anderes als die Spannung zwischen linker Kondensatorplatte und dem Punkt P_2.
Zwei Punkte, zwischen denen die Spannung 0 ist, liegen in obiger Abbildung auf einer Parallelen zu den Kondesatorplatten.
Auf allen Punkten dieser Parallelen hätte die Ladung die selbe "elektrische potentielle Energie" bzw. das selbe Potential, da keine Arbeit verrichtet werden muss, um sie von einem Punkt zu einem anderen entlang einer dieser Parallelen zu verschieben. Man nennt die Parallele daher Äquipotentiallinie.
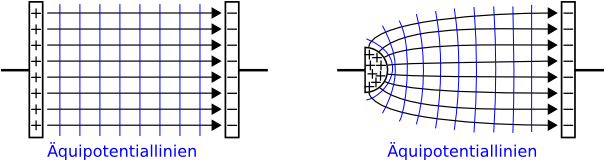
In der linken obigen Abbildungen haben also alle Punkte entlang derselben blauen Linie das selbe Potential. Zwischen ihnen ist die Spannung Null. Die blauen Linien sind parallel zur Kondensatorplatte. Verschiebt man entlang einer blauen Linie eine Ladung, muss also keine Arbeit verrichtet werden.
In der rechten oberen Abbildung ist die positiv geladene Platte des Kondensators halbkreisförmig. Dadurch verformt sich das elektrische Feld. Die Äquipotentiallinien passen sich dem Verlauf des Feldes entsprechend an: Da ausschließlich bei einem zu den Feldlinien senkrechten Transport von Ladungen keine Arbeit verrichtet wird, verlaufen die Äquipotentiallinien immer senkrecht zu den Feldlinien des elektrischen Feldes.
Der Begriff des Potentials wird später noch eine wichtige Rolle spielen.
Zusammengefasst:
- Linien eines Feldes, zwischen deren Punkte die Spannung Null ist, nennt man Äquipotentiallinien. Im Dreidimensionalen nennt man entsprechende Flächen Äquipotentialflächen.
- Äquipotentiallinien (bzw. Flächen) verlaufen immer senkrecht zu den Feldlinien.
- Im homogenen Feld liegen die Äquipotentiallinien parallel zueinander.
Der Zusammenhand zwischen U, E und d beim Plattenkondensator
In diesem Abschnitt wollen wir eine Formel finden, mit der man die Stärke des elektrischen Feldes zwischen zwei Kondensatorplatten berechnen kann.
Der Abstand zweier Kondensatorplatten sei d. Diese sind an der Gleichspannung U angeschlossen und werden von dieser Spannungsquelle geladen.
Gedanklich transportieren wir jetzt eine Probeladung q von einer Platte des Kondensators zur anderen Platte.
Darin verrichtet das Feld auf die Probeladung q, die Arbeit
Daraus folgt für die Spannung zwischen den Platten:
Stellen wir diese Gleichung um, können wir bereits die Feldstärke E aus der am Kondensator anliegenden Spannung U und dem Plattenabstand d berechnen:
Hieraus erkennen wir auch direkt die Einheit der elektrischen Feldstärke. Sie hat keine eigene Bezeichnung, sondern lässt sich nur durch die uns bekannten Einheiten wie folgt darstellen.
D.h. über die an einem Plattenkondensator anliegende Spannung lässt sich eine Aussage über die Stärke des E-Feldes machen.
Zusammengefasst:
- Für die Spannung zwischen zwei Punkten im elektrischen Feld der konstanten Feldstärke E, welche den Abstand d voneinander haben, gilt:
Der Zusammenhang zwischen Flächenladung und Feldstärke
Experiment: Eine Metallscheibe mit dem Radius r= 0,05m wird an die Innenfläche einer Kondensatorscheibe gedrückt. Die auf dieser Fläche befindlichen Ladungen werden mit der Scheibe abgehoben. Die auf der Scheibe befindliche Ladung wird gemessen.
Wovon hängt es vermutlich ab, wie viel Ladung auf die Scheibe passt?
Vermutungen:
- Je größer die Spannung U, desto größer die Ladung Q auf der Metallscheibe (d konstant)
- Je größer der Abstand d, desto kleiner die Ladung Q auf der Metallscheibe (U konstant)
Durchführung des Experiments, Meßwerte:
| Spannung U | Abstand d | Feldstärke E = U/d | Ladung auf Scheibe Q | Sigma |
| 2500 V | 4 cm | 62500 V/m | 4,7 nC | 5,89 * 10^-7 C/m^2 |
| 4000 V | 4 cm | 1000000 V/m | 7,1 nC | 9,04 * 10^-7 C/m^2 |
| 5500 V | 4 cm | 137500 V/m | 9,5 nC | 1,2 * 10^-6 C/m^2 |
| 2500 V | 2 cm | 125000 V/m | 9,5 nC | 1,2 * 10^-6 C/m^2 |
| 2500 V | 6 cm | 41666,7 V/m | 2,8 nC | 3,57 * 10^-7 C/m^2 |
| 4000 V | 6 cm | 66666,7 V/m | 4,1 nC | 5,22 * 10^-7 C/m^2 |
| 5500 V | 6 cm | 91666,7 V/m | 5,4 nC | 6,88 * 10^-7 C/m^2 |
| 10000V | 6 cm | 166666,7 V/m | 11,1 nC | 1,41 * 10^-6 C/m^2 |
Ergebnis:
Unsere Vermutungen sind korrekt. Zusätzlich können wir folgende Aussage machen, welche beide Vermutungen kombiniert:
Die mit der Metallscheibe abgehobene Ladung Q ist proportional zur Stärke des elektrischen Feldes E.
Zusammengefasst:
- Die Größe der Ladung auf der Innenfläche eines Kondensators ist proportional zur elektrischen Feldstärke E im Innern des Kondensators.
Die Flächenladung hängt tatsächlich nur vom Feld E ab!!
Experiment:
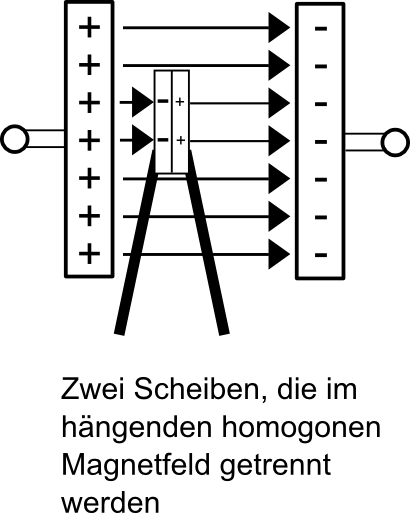
Zwei Scheiben werden im homogenen Feld E senkrecht zu den Feldlinien zusammen gehalten. Wegen Influenz kommt es zu der in der Abbildung gezeigten Ladungstrennung.
Die Scheiben werden im Feld getrennt und die Ladungen gemessen.
Ergebnis und Schlussfolgerung:
Auf den Scheiben ist genau so viel Ladung wie auf einer gleich großen Fläche der Kondensatorplatten.
Da an den Scheiben keine Spannung anliegt, sondern diese nur mit dem E-Feld wechselwirken, folgt:
Die Menge an Ladungen auf einer Metallfläche hängt nur von der Stärke des elektrischen Feldes ab, in welchem sich die Metallfläche befindet.
Zusammengefasst:
- Die Ladungsmenge, die sich auf einer Metalloberfläche bildet, ist proportional zur elektrischen Feldstärke des Feldes, welches an dieser Oberfläche endet.
Die Flächenladungsdichte
Die Flächenladungsdichte ist ein Maß dafür, wie dicht die Ladungen auf einer Fläche sitzen:
Sie hat die Einheit
Während die Ladungsmenge auf einer Platte von ihrer Fläche abhängt, ist die Flachenladungsdichte von der dieser Größe unabhängig.
Bei gleicher Fläche gilt:
Je größer die Flächenladungsadichte, desto größer die Ladung Q.
Zusammengefasst:
- Die Flächenladungsdichte ist als Ladung pro Fläche definiert.
Der Zusammenhang zwischen Flächenladungsdichte und Feldstärke
Im Experiment konnten wir zeigen, dass die Ladung auf einer Scheibe proportional zur Feldstärke steigt. Da die Fläche konstant bleibt, steigt auch die Flächenladungsdichte proportional zur Feldstärke E, wie man aus der Tabelle des vorvergangenen Abschnitts erkennen kann.
Der neu eingeführte Proportionaltätsfaktor
heißt "elektrische Feldkonstante". Sie kann mit den Messwerten aus der genannten Tabelle berechnet werden:Dieser Konstanten kommt in der Physik eine besondere Bedeutung zu. Bei gleicher Feldstärke wird durch diese Konstante bestimmt, wie viele Ladungen durch die Feldkräfte auf eine Fläche gezogen werden. Sie ist somit eine Zahl, welche die Stärke der elektrischen Wechselwirkung bestimmt. Von ihr alleine hängt es ab, wie stark sich geladene Körper anziehen oder abstoßen, wenn sie geladen sind. Da fast alle Vorgänge des Alltags von den elektrischen Kräften abhängen, hat die Konstante eine große Bedeutung für unser Leben, ja sogar für unsere Existenz.
Zusammengefasst:
- Die Flächenladungsdichte einer Metalloberfläche ist proportional zur Stärke des Feldes E, in welcher sich die Oberfläche befindet.
- Die Proportionalitätskonstante wird elektrische Feldkonstante genannt. Es handelt sich um eine Naturkonstante:
Die Kapazität eines Kondensators
Wie viele Ladungen passen auf einen Plattenkondensator?
Wenn wir die Plattenfläche A kennen, können wir diese Frage leicht mithilfe der Flächenladungsdichte und bekannter mathematischer Zusammenhänge beantworten.
Bei einem Kondensator mit bekannter Fläche A und bekanntem Plattenabstand d können wir mit dieser Formel also berechnen, wie viele Ladungen Q auf den Platten sitzen, wenn die Spannung U am Kondensator anliegt.
Wir führen folgende Abkürzung ein
wodurch sich die Formel für die Kondensatorladung Q stark vereinfacht ausdrücken lässt:
Von der Größe
hängt es ab, wie viele Ladungen bei einer bestimmten Spannung auf den Kondensator passt. Sie heißt deshalb auch Kapazität des Kondensators und wird mit dem Symbol C abgekürzt. Die Kapazität hat auch eine eigene Einheit, das Farad. Es setzt sich wie folgt aus den bekannten Einheiten zusammen.Eine Kapazität von 1 Farad bedeutet,dass der Kondensator bei einer Spannung von 1 Volt die Ladung 1 Coulomb speichert.
In technischen Anwendungen möchte man häufig besonders viele Ladungen speichern. Daher die Frage: Unter welchen Bedingungen ist die Kapazität eines Kondensators besonders groß?
Eine Formel sagt mehr als tausend Worte...
- Wenn die Fläche A möglichst groß ist.
- Wenn der Plattenabstand d möglichst klein ist.
Zusammengefasst:
- Die Kapazität eines Kondensators ist ein Maß für die Größe eines Kondensators.
- Für die Ladung Q, die bei einer anliegenden Spannung U auf den Kondensator passt, gilt die Beziehung
Dieelektrizitätszahl
Gibt es weitere Möglichkeiten, die Kapazität eines Kondensators zu vergrößern?
Experiment: \\ Wir messen die Kapazität ein und desselben Plattenkondensators unter zwei Bedingungen:
- Mithilfe der im vergangenen Abschnitt hergeleiteten Formel wird die Kapazität des Kondensators bestimmt.
- Anschließend wird eine Plexiglasscheibe zwischen die Kondensatorplatten eingeschoben und der Vorgang bei gleicher Spannung U wiederholt:
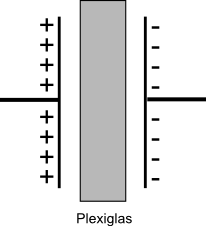
Ergebnis: Durch die Plexiglasscheibe hat sich die Kapazität um einen Faktor, den wir mit dem Symbol
abkürzen, erhöht. Diese Zahl ist vom eingeschobenen Stoff abhängig und wird Dielektrizitätszahl genannt. Schieben wir Materialien mit besonders hohen Dielektrizitätszahlen zwischen die Platten eines Kondensators, können wir seine Kapazität folglich weiter erhöhen. Hier die Dielektrizitätszahlen ausgewählter Materialien:| Stoff | Dielektrozitätszahl |
| Luft | 1,00058 |
| Wachs | 2 |
| Glas | 5 bis 16 |
| Alkohol | 26 |
| Wasser | 81 |
| Keramik mit BgSr | 10000 |
Daraus folgt für die Kapazität eines Kondensators
und für seine Flächenladungsdichte:
Allgemein nennt man Stoffe, die auf die beschriebene Art die Kapazität von Kondensatoren erhöhen können, Dielektrika.
Zusammengefasst:
- Durch Dielektrika kann die Kapazität von Kondensatoren um einen materialabhängigen Faktor epsilonr erhöht werden, welcher Dielektrizitätszahl genannt wird.
- Für Kapazität und Flächenladungsdichte eines Plattenkondensators mit Fläche A und Plattenabstand d gilt:
Mikroskopische Betrachtung von Isolatoren in elektrischen Feldern
Weshalb erhöht sich die Kapazität eines Plattenkondensators, wenn man ein Dielektrikum in sein Feld schiebt?
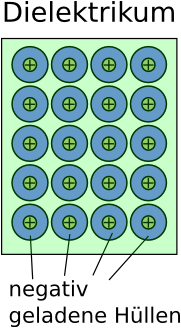
Die Atome der Isolatoren bestehen aus einem positiv geladenen Kern (+) und einer negativ geladenen Hülle um den Kern herum (grau schraffiert).
Zwar sind die Elektronen der Hülle in Elektronenwolken an ihre Atome gebunden, allerdings verschieben sich die Elektronenwolken leicht zur positiven Platte. Dadurch wird die in der Abbildung linke Isolatorseite negativ, die rechte positiv geladen. Diese Ladungen ziehen zusätzliche Ladungen auf die Platten des Kondensators.
Das durch die Polarisationsladungen des Isolators entstehende innere Feld schwächt im Isolator das durch den Kondensator verursachte Feld ab.
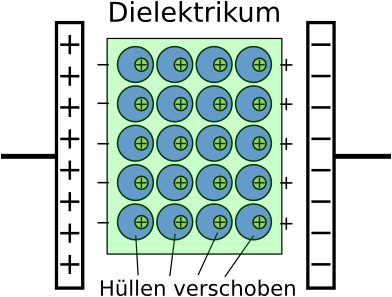
Zusammengefasst:
- Durch innermolekulare und -atomare Ladungsverschiebungen vergrößern Dielektrika die Kapazität von Kondensatoren.
Die in Kondensatoren gespeicherte Energie
Bräuchte man zum Laden eines Kondensators immer die gleiche Spannung U, könnte man leicht ausrechnen, wie viel Energie auf ihn gespeichert wäre, wenn man die Ladung Q auf ihn lädt; denn Spannung ist schließlich als Arbeit pro Ladung definiert.
Gehen wir zunächst einmal davon aus, ein Kondensator würde fortlaufend mit einer gleich bleibenden Spannung geladen werden. Dann würde die Ladung bei konstanter Spannung immer weiter ansteigen und in einem Diagramm, bei welchem auf die x-Achse die Ladung Q und auf die y-Achse die anliegende Spannung aufgetragen wird, würde wie folgt aussehen.
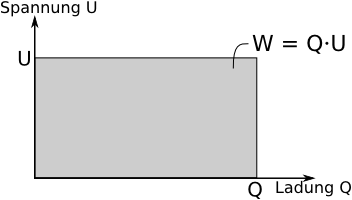
Wird der Kondensator bis zur Ladung Q geladen, so würde für diesen Vorgang die Arbeit Q*U verrichtet werden. Dies entspricht aber gerade der Fläche im Q-U-Diagramm!
Das heißt, wir können die verrichtete Arbeit aus einem solchen Diagramm leicht ablesen, indem wir die vom Graphen mit der x-Achse eingeschlossene Fläche bestimmen.
Die Spannung bleibt beim Laden eines Kondensators aber entgegen der oben gemachten Annahme nicht gleich: Man benötigt zum Laden eines Kondensators eine um so größere Spannung, je mehr Ladung sich auf ihm befindet. Wegen
benötigt man die Spannung , die linear mit Q anwächst. Das Q-U-Diagramm sieht also in Wirklichkeit wie folt aus: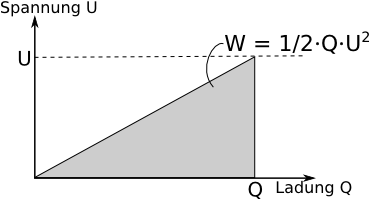
Wie viel Arbeit wird beim Laden also verrichtet? Zum Glück haben wir gerade gesehen, dass die verrichtete Arbeit der Fläche im Diagramm entspricht. D.h.:
Zusammengefasst:
- In Kondensatoren wird elektrische Energie gespeichert. Die Menge an elektrischer Energie lässt sich über folgende Formel berechnen:
Die Energiedichte des elektrischen Feldes
Faraday ging davon aus, dass die Energie eines Kondensators nicht auf den Platten, sondern im Feld des Kondensator gespeichert ist und somit den Zwischenraum zwischen den Platten durchsetzt:
Wenn dies tatsächlich so ist, müsste die in einem Kondensator gespeicherte Energie proportional zum Volumen des Zwischenraums sein, den das Feld durchsetzt.
Mit
und
erhalten wird durch Einsetzen:und wegen V = A * d
Die im Kondensator gespeicherte Energie ist also tatsächlich proportional zum Volumen V. Dies ist ein weiteres Indiz dafür, dass Faraday mit seiner Feldtheorie Recht hatte!
Wenn die Energie im Feld steckt, können wir auch eine Energiedichte angeben!
Die Energiedichte des elektrischen Feldes gibt in diesem Zusammenhang an, wie viel Energie pro Volumeneinheit im Feld gespeichert ist:
Zusammengefasst:
- Die in einem Kondensator gespeicherte Energie sitzt im Feld des Kondensators.
- Die Energie, die pro Raumvolumen gespeichert wird, nennt man Energiedichte. Ist die Stärke des Feldes E, so lässt sich die Energiedichte durch die folgende Formel berechnen.
Die Elektronenkanone
In den vorhergehenden Abschnitten haben wir Elektronen als "Stoff" erkannt, der beim elektrischen Strom durch die Leitung fließt. Es sind frei bewegliche Ladungsträger. Wir haben auch bereits eine Methode kennen gelernt, sie mithilfe der Glühemission aus einen Glühdraht zu befördern.
In diesem Abschnitt wollen wir sie nicht nur aus einem Glühdraht herauslösen - unser Ziel ist es, einen Strahl aus reinen Elektronen zu erzeugen! Und wie machen wir das? - Nun, die folgende Abbildung gibt Aufschluss darüber!
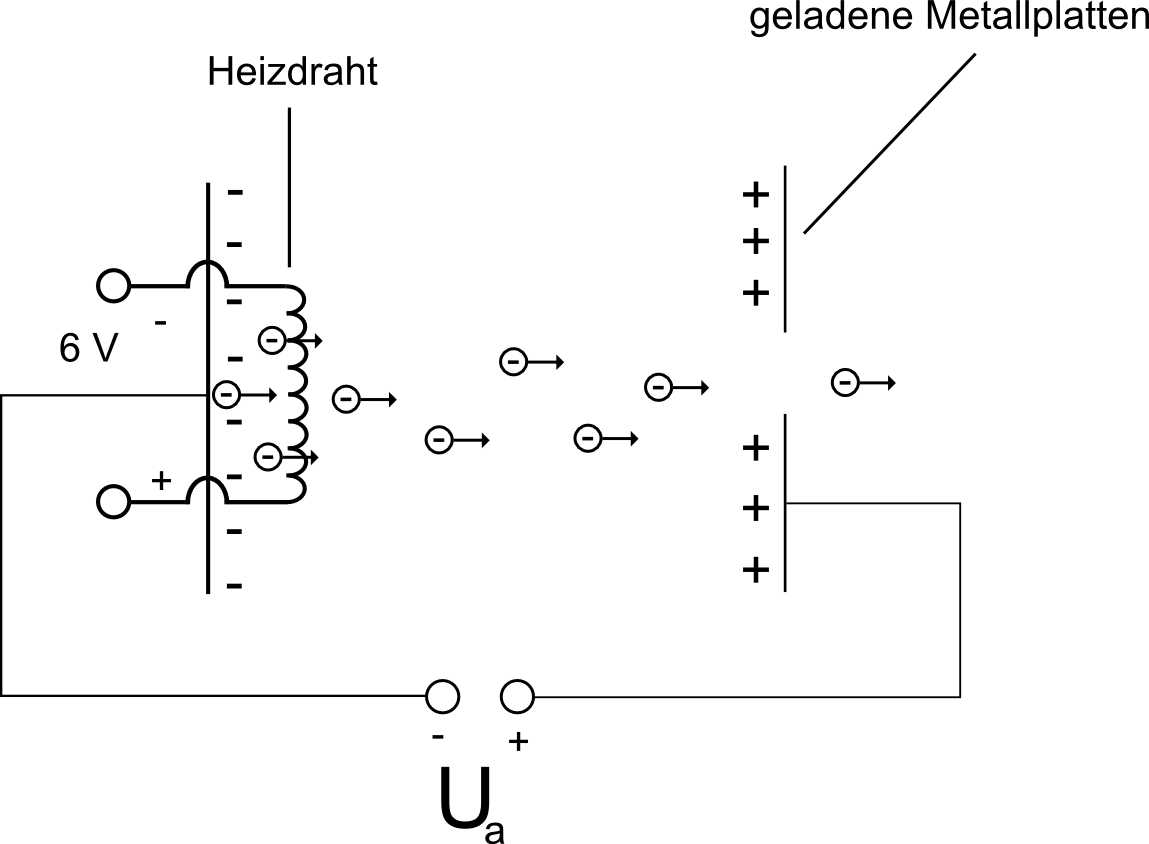
Die Idee:
- Über einen Glühdraht Eletronen auslösen
- Die Elektronen im elektrischen Feld zweier Kondensatorplatten beschleunigen
- Die Elektronen durch eine Lücke in der hinteren Platte rausfliegen lassen
... wenn wir das so machen: Wie schnell werden die Elektronen dann?
Berechnung der Geschwindigkeit der Elektronen:
- Weil die Elektronen die Spannungsdifferenz U_a durchlaufen, verrichtet das Feld an ihnen die Beschleunigungsarbeit
- Durch die Beschleunigungsarbeit wird elektrische Energie in kinetische Energie umgewandelt. Am Ende der Beschleunigungsphase hat das Elektron mit der Geschwindigkeit v die Energie:
- Nach der Beschleunigungsphase entspricht die kinetische Energie der Beschleunigungsarbeit, die an dem Elektron verrichtet wurde.
- Umstellen nach v ergibt:
Experiment und Beobachtung:
Die Elektronen in einem Experiment werden mit U_a=5000V beschleunigt. Wir sehen am Leuchtschirm einen Punkt, der durch den Aufprall der Elektronen verursacht wird.
Berechnung der Geschwindigkeit:
Hierzu benötigen wir die Ladung und die Masse eines Elektrons. Später wird gezeigt, wie man die Größen experimentell ermittelt - hier nutzen wir sie, um die Geschwindigkeit der Elektronen im Elektronenstrahl zu berechnen:
Ladung:
Masse:
Hinweise:
- Bei noch höheren Beschleunigungsspannungen muss relativistisch gerechnet werden.
- In der Literatur wird die "Elektronenkanone" in der Regel Elektronenröhre genannt.
- Der Elektronenstrahl wird in der Literatur oft Kathodenstrahl genannt.
Zusammengefasst:
- Mit Elektronenröhren können freie, mit hoher Geschwindigkeit fliegende Elektronen erzeugt werden.
- Der so entstehende Elektronenstrahl wird Kathodenstrahl genannt.
Die Einheit Elektronenvolt
Ein Elektronenvolt (kurz: eV) ist die Arbeit, die ein elektrisches Feld an der Ladung 1e verrichtet, wenn diese von einem Punkt zu einem anderen Punkt mit der Spannung 1V zwischen diesen beiden Punkten bewegt wird. Durchläuft ein Teilchen der Ladung 1e die Spannung, so erhöht sich seine kinetische Energie um 1eV.
Das Ablenksystem einer Brownischen Röhre
Die Elektronenkanone aus Aufgabe 25 erzeugt sogenannte Elektronenstrahlen, die auch Kathodenstrahlen genannt werden. In alten Fernsehrgeräten leuchten diese Kathodenstrahlen die Mattscheibe aus, indem sie sehr schnell zeilenförmig von links oben nach rechts unten gelenkt wurden und auf der Scheibe an der jeweiligen Position einen Punkt zum Leuchten brachten. Heute findet die Ablenkung der Sttrahlen noch in Elektroskopen Anwendung. Doch wie könnte man solche Kathodenstrahlen ablenken?
Exp: Ein Kathodenstrahl wird von einem homogenen el. Feld abgelenkt.
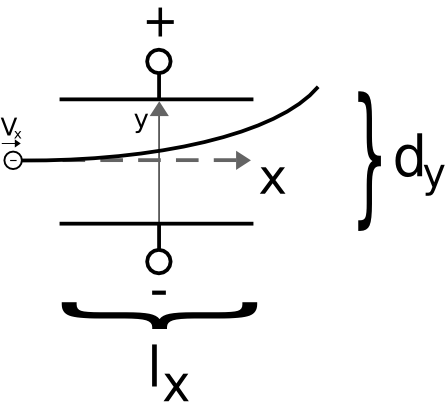
Flugbahnberechnung:
- Die Elektronen wurden durch die Beschleunigungsspannung Ua auf die Geschwindigkeit in x-Richtung
- Wegen der Platten wirkt in y-Richtung die Kraft
- Diese beschleunigt die Elektronen gemäß
- In x-Richtung legen die Elektronen in der Zeit t die Strecke zurück. Für die Breite der Platten benötigen sie daher die Zeit .
- Während dieser Zeit beschleunigen sie mit a_y. Sie erreichen nach der Zeit t_p die Geschwindigkeit in y-Richtung:
- Am Ende der Kondensatorplatten haben die Elektronen dann den folgenden Weg in y-Richtung zurückgelegt:
- Als nächstes ersetzen wir v_x durch die Geschwindigkeitsformel ganz oben und kürzen...
Dies ist die Bahngleichung des Elektrons. Ist die Plattenlänge l_x, der Plattenabstand d_y, die Ablenkspannung U_y und die Beschleunigungsspannung U_a bekannt, lässt sich jeder Punkt, den die Elektronenbahn nimmt, darüber berechnen. Anhand der Gleichung erkennen wir das überraschende Ergebnis:
Der Verlauf des Kathodenstrahls in y-Richtung ist unabhängig von Masse und Ladung der Ladungsträger.
Zusammengefasst:
- Kathodenstrahlen können mithilfe des Ablenksystems einer Brown'schen Röhre auf genau berechenbaren Bahnen abgelenkt werden.